Best et worst case scénarios pour un déconfinement de pandémie

S’il y a bien une interrogation dans tous nos esprits en ce moment, c’est celle-là : Quand ce cauchemar va-t-il bientôt se terminer ?

Il apparaît aujourd’hui de plus en plus évident que le Covid-19 fera partie de nos vies quotidiennes de la même manière que la grippe ou la varicelle. L’éradication de ces dernières n’a jamais pû être réalisée malgré des vaccins et un suivi de leurs épidémies saisonnières respectives.

On peut être tenté de penser qu’il est possible d’éliminer ce virus au Maroc puisque le nombre d’infectés reste faible et le contrôle sanitaire strict et responsable. Mais d’une part, l’apparition régulière de clusters montre que le caractère asymptomatique important des symptômes du virus le rend très difficile à suivre. Et d’autre part, le fait même que d’autres pays aient choisi de se limiter à dompter le virus nous laissera toujours exposés lorsque les frontières seront rouvertes et le commerce mondial relancé. Sauf changement global de paradigme économique.

Alors que faire ?

Lever le confinement. Comme de nombreux pays asiatiques échaudés par de précédentes pandémies, nous devrons également apprendre à modifier nos usages sociaux et professionnels afin de contrôler naturellement la propagation du virus sans éreinter le système sanitaire. Cela suppose des outils technologiques et surtout un grand sens de la responsabilité.

En sommes-nous capable ? Avons-nous même le choix ?

Au regard de cette dernière idée, il me semble que le Covid-19 est un virus de société. Il terrassera les plus inciviques et impréparées mais ne sera qu’une grippe de plus pour les pays les plus robustes et immunisés (au sens sociétal). Seules les sociétés qui auront su s’adapter (ou s’isoler durablement mais est-ce encore possible ?) ne feront pas le sacrifice de leur système de santé et de centaines de milliers de morts pour atteindre l’immunité collective.

Quid de la pandémie en situation de déconfinement

Le déconfinement signifie notamment la levée des restrictions de libertés publiques individuelles et la reprise progressive des activités économiques. Le but est de permettre à la société de refonctionner normalement tout en maîtrisant la situation pandémique. Le déconfinement et ses modalités d’application ne sont qu’une décision politique qu’il convient d’acter. La vraie question est comment évoluera la pandémie dans ce cas ?

Voici quelques scénarios de déconfinement modélisables à l’échelle de notre pays qui peuvent servir à illustrer la complexité de la dynamique du Covid-19 actuel. Attention, certains scénarios sont irréalistes pour ne pas dire fantaisistes, la visée de cet article restant purement pédagogique.

Index

Pour faciliter la navigation dans cet article

• Modèle développé
• Hypothèses choisies
• Scénario X - Ce n’est qu’une grippe
• Scénario 0 - Éradication
• Scénario 1 - Déconfinement one shot
• Scénario 2 - Déconfinement yo-yo
• Scénario 3 - Immunité collective
• Scénario 4 - Incivilités individuelles
• Scénario 5 - Incivilités sociales
• Scénario 6 - Les cas importés
• Scénario 7 - Immunité temporaire
• Remarques méthodologiques
• Next steps
• Code
• Mises à jour
• Sources

Le modèle utilisé

Dans un précédent article, je décrivais brièvement les prémisses d’une modélisation de pandémie basée sur la simulation du comportement individuel de chacun d’entre nous. Cette simulation avait ses forces et ses faiblesses qu’il a fallu résoudre. L’idée était de rendre le modèle le plus vraisemblable possible. Reprenons les bases.

Considérons une population constitué d’individus. Nous affectons à chaque individu :

• Son âge qui détermine son taux de mortalité du au virus ainsi que la probabilité qu’il soit hospitalisé et donc isolé et non contagieux pour ses semblables
• Sa maison placée aléatoirement sur une grille
• La possibilité de faire du télétravail versus l’obligation d’aller sur son lieu de travail
• Un lieu de travail placé préférentiellement sur les axes centraux de la grille
• Un indice de comportement caractérisant son respect des consignes sanitaires et de confinement
• La caractéristique adulte ou enfant : seul un adulte par foyer va dans une épicerie et seuls les adultes travaillent

On attribue à chaque maison :

• Les k épiceries les plus proches de la maison (k étant un paramètre à choisir). L’individu est censé aller à la plus proche mais on lui donnera la possibilité d’aller à des épiceries plus éloignées ce qui est un facteur de non respect du confinement
• Un quartier qui est choisi dans un découpage uniforme de la grille en blocs de forme carrée

Chaque individu obligé d’aller à son lieu de travail part de sa maison et passe par un nombre de blocs. Toute personne passant par le même bloc la même journée a un risque d’être contaminée. C’est une façon de modéliser les transports publics que nous allons moduler avec une pondération bien entendu assez faible.

L’épidémie se propage

• à la maison chaque soir parmi tous les membres du foyer selon une probabilité de contagion familiale
• à l’épicerie les deux jours du weekend uniquement pour un seul adulte par foyer selon une probabilité de contagion à l’épicerie
• au lieu de travail et dans les transports publics chaque jour de la semaine uniquement pour les non télé-travailleurs selon une probabilité de contagion professionnelle et une probabilité de contagion des transports publics
• Une personne contagieuse ne peut infecter qu’au plus un nombre défini (en paramètre) de personnes dans les transports publics

Ces quatre dernières probabilités sont des paramètres globaux qui représentent l’état du confinement.

Chacune de ces probabilités sera pondérée par l’indice individuel de comportement (matérialisé par les précautions sanitaires, l’usage du masque etc.)

Concernant les états des individus, ils peuvent passer :

• De sain à infecté s’il y a contamination
• D’infecté non contagieux à infecté contagieux si la durée d’infection dépasse en nombre de jour la durée d’incubation du virus
• D’infecté à hospitalisé si l’individu est suffisamment âgé (selon une table de paramètres d’hospitalisation)
• D’infecté à isolé si l’individu fait partie de la famille d’une personne hospitalisée. Il n’a alors plus le droit d’aller ni au travail ni à l’épicerie
• D’infecté ou hospitalisé ou isolé à immunisé si l’individu l’emporte sur le virus (selon une table de mortalité)
• D’infecté ou hospitalisé ou isolé à mort si l’individu est suffisamment âgé (selon une table de mortalité)
• D’immunisé à sain si le niveau d’immunité de l’individu a beaucoup baissé (selon une durée de vie des anticorps de chaque individu)

Revenir à l’index

Les hypothèses et raccourcis assumés

Il n’y a pas de modélisation sans hypothèses.

Les paramètres liés à l’âge

• Un âge est attribué à chaque individu sur la base des pyramides de population de 2019 suivantes ^[8]
• Le taux de mortalité est basé sur les données empiriques Covid-19 suivantes ^[6]. Par exemple les 50-59 ans ont un taux de mortalité de 1.3% alors que le taux monte à 14,8% pour les plus de 80 ans. Dans une simulation idéale, il faudrait modéliser les maladies chroniques, les problèmes cardio-vasculaires etc. Disons qu’en première approximation, l’âge est un bon prédicteur
• La probabilité d’hospitalisation utilise les données synthétiques Covid-19 suivantes ^[7]. Pour les 30-39 ans, ce taux correspondait à 2,5% au 11 avril 2020. Les chiffres sont mis à jour régulièrement sur ce site
• Lorsque le nombre d’hospitalisation dépasse le nombre de lits en soins intensifs (qui est de 85 par million d’habitants au Maroc ^[13]), les taux de mortalité des personnes hospitalisées sont multipliés par le rapport de l’hospitalisation sur le nombre total de lits. S’il faut hospitaliser 20 personnes pour 5 lits disponibles, on aura par exemple un taux de mortalité multiplié par 4. Sévère mais probablement réaliste.

Les paramètres liés à la vie du virus dans le corps

• A partir de l’entrée du virus dans le corps, l’individu devient contagieux (fin de la période d’incubation) au bout de 4 à 6 jours. Cela se base sur l’étude suivante ^[9] qui donne dans un intervalle de confiance de 95% une durée de 4,5 à 5,8 jours. Au-delà, l’individu devient un danger pour les autres
• La même étude donne une durée moyenne pour l’apparition des premiers symptômes et donc logiquement la prise en charge hospitalière lorsque nécessaire (selon l’âge). Cette durée varie de 8 à 16 jours ^[9]
• L’infection virale doit donner lieu à la décision tragique de vie ou de mort. Cette décision se fait au bout de 8 à 31 jours sur la base de l’étude suivante ^[3]
• La question de l’immunité est débattue aujourd’hui et à priori on annonce un niveau d’immunité humaine plus important que pour la grippe saisonnière en raison du faible nombre de mutations annuelles spontanées du Covid-19. Ce serait une bonne nouvelle pour l’arrivée d’un vaccin l’année prochaine. Voir l’article suivant ^[9]. Ainsi, nous pouvons octroyer par défaut une immunité infinie aux individus. Nous étudierons un scénario effrayant avec une immunité très courte (30 à 60 jours) si le virus venait à muter très rapidement par exemple

Les paramètres choisis en situation de vie normale

• 58% des adultes sont en télé-travail (ou chômage) (à partir de l’étude du HCP qui donne un taux d’emploi de 42% en 2019 en faisant fi des disparités homme/femme et urbain/rural ^[11] )
• 50% de probabilité de contagion à la maison
• 10% de probabilité de contagion dans les transports publics
• 10% de probabilité de contagion au travail
• 20% de probabilité de contagion dans les épiceries
• 30% des individus vont à l’épicerie la plus proche, les 60% restant vont dans les autres épiceries plus éloignées

Les paramètres choisis en situation de confinement normal

• 98% des adultes sont en télé-travail
• 50% de probabilité de contagion à la maison pour tous les individus du foyer (il n’y a pas de raison pour que cela change foncièrement)
• 1% de probabilité de contagion dans les transports publics pour ceux qui traversent les mêmes blocs
• 1% de probabilité de contagion au travail pour tous les collaborateurs d’une même entreprise
• 2% de probabilité de contagion dans les épiceries pour tous les adultes qui vont faire leurs courses au même endroit
• 95% des individus respectent l’obligation d’aller à l’épicerie la plus proche, les 5% restant vont aux autres épiceries plus éloignées

Autres paramètres

• Il y a une épicerie pour 20 maisons
• A chaque maison lui est associée 3 épiceries par ordre de proximité
• La grille géographique est constituée de 20 blocs par axe : Cela donne 400 blocs (ou mini-quartiers) au total
• Sauf mention du contraire, la population sera de 35000 individus et chaque instance de simulation durera 180 à 360 jours
• Un foyer est composé de 1 à 10 personnes et le nombre d’individus dedans suit une distribution gaussienne de moyenne 4.52 personnes (données HCP ^[12] )
• La taille des entreprises se divise en TPE (1 à 3 employés), PME (4 à 15 employés) et GE (16 à 30 employés). Les nombres sont faibles car la taille de population étudiée l’est également
• Une personne infectée n’est en contact qu’avec au plus 10 personnes dans les transports en commun
• L’indice de comportement est compris entre 50% et 150% choisi aléatoirement dans une loi normale de moyenne 100%. Un comportement de 50% est bon car il y a 2 fois moins de risque. A l’inverse, 150% dénote d’un comportement irresponsable. L’idée est de modéliser aussi la diversité des comportements
• Par défaut, 20 simulations seront lancées et sauf mention du contraire dans le cas de la grille avec les 9 simulations côte à côte, les résultats affichés seront la moyenne des 20 simulations
• 5 personnes seront initialement infectées pour simuler le lancement de l’épidémie

Tous ces paramètres sont ajustables et me paraissent vraisemblables.

Revenir à l’index

Évaluons à présents quelques scénarios

Le code associé à chaque scénario sera inclus dans l’article afin de permettre aux plus curieux de reproduire les expériences et éventuellement les ajuster en fonction des idées.

Scénario X : Ne rien faire (dit scénario de la grippe saisonnière)

La pandémie commence et les autorités décident que le virus n’est qu’une simple grippe ^[23]. Aucune modification de comportement n’est demandée à la population. Les cafés, restaurants et entreprises restent opérationnels.

Utilisons les paramètres de situation normale et analysons l’évolution de la situation :

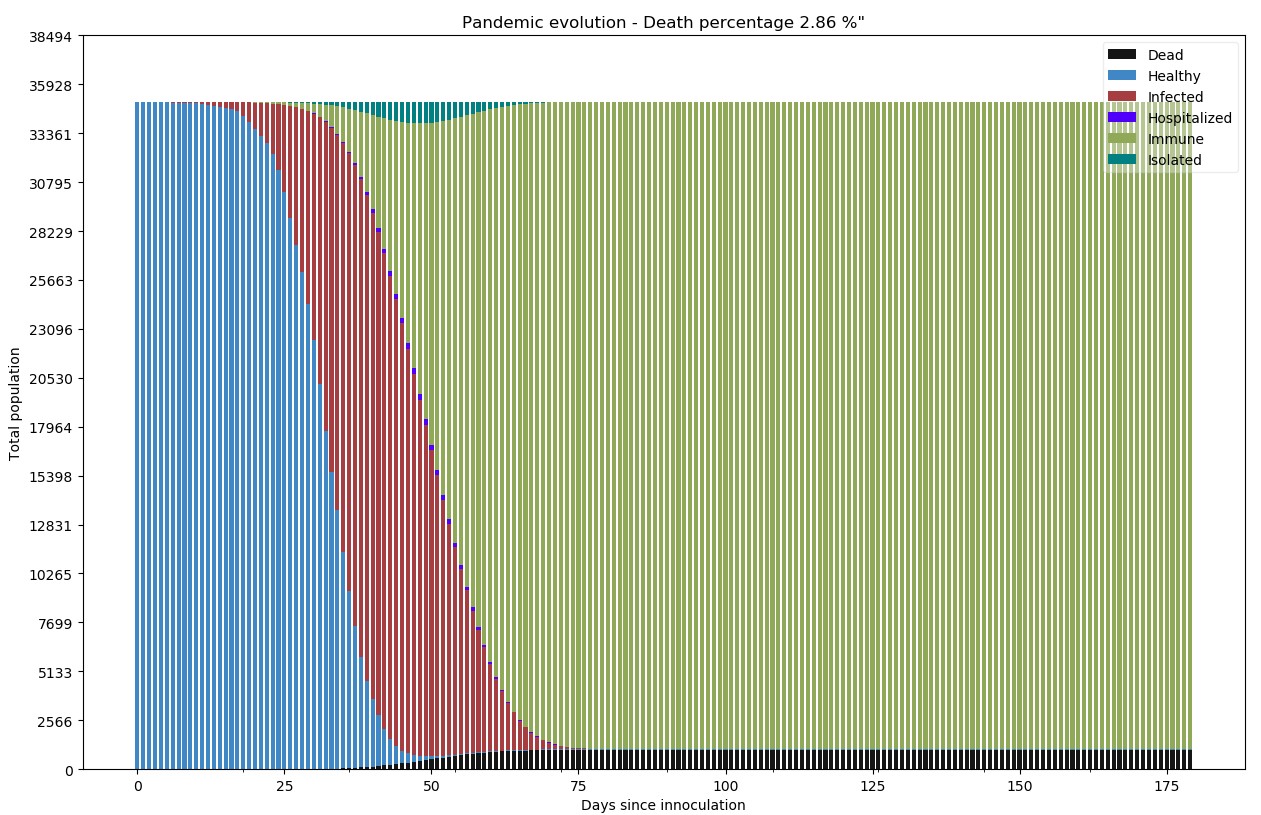
Ce graphe représente l’état de la population globale. En bleu les personnes en bonne santé, en rouge les personnes infectées, en noir les personnes décédées, en violet les personne hospitalisées et en vert les personnes immunisées.

C’est bien évidemment une hécatombe. Il faut moins de 50 jours pour que l’ensemble de la population ait été infectée. Le résultat est environ une immunité quasi totale et le décès de 3% de la population. La société s’ampute de ses personnes les plus fragiles et âgées pour tourner la page de la pandémie.

Si on s’intéresse à la moyenne sur les 20 simulations du nombre d’hospitalisations et de nouveaux cas :

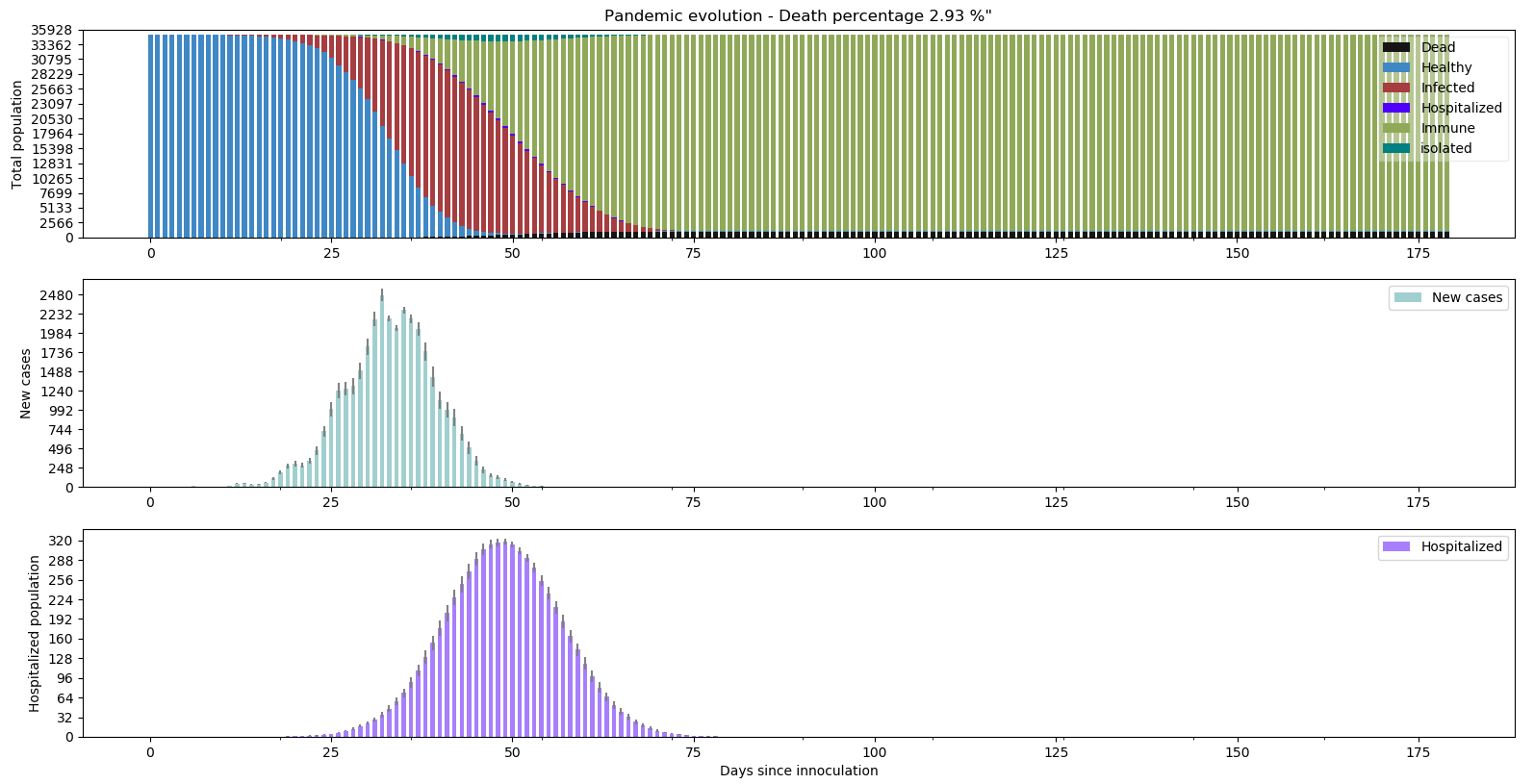
• Le 2ème graphe correspond au nombre de nouveaux infectés par jour
• Le 3ème graphe correspond au nombre de personnes à l’hôpital par jour

Une remarque importante me vient à l’esprit :

• Le nombre de mort est peut être très faible comparativement à un virus comme celui d’Ebola (50% à 90%), mais quand on constate la courbe d’hospitalisation, il y a clairement un pic au bout du 50ème jour qui conduit inévitablement à une surcharge des infrastructures sanitaires. Rapportée à un population de 35000 individus, le Maroc n’aurait que 4 lits intensifs. Or on constate des pics à 290 lits utilisés ici soit plus de 90 fois notre capacité maximum. Notre modèle multiplie donc par 90 les taux de mortalités pour les personnes “hospitalisées” (qui le sont dans des conditions difficiles du fait du manque de lits) ce qui donne en moyenne les 3% de population décédée.

La rapidité de l’évolution de la maladie prouve les caractéristiques exponentielle d’une pandémie. On caractérise souvent cet aspect par un coefficient dit le R0. C’est le nombre moyen de personnes contaminées par une personne infectée. Au delà de 1, l’épidémie devient une pandémie quasiment incontrôlable :

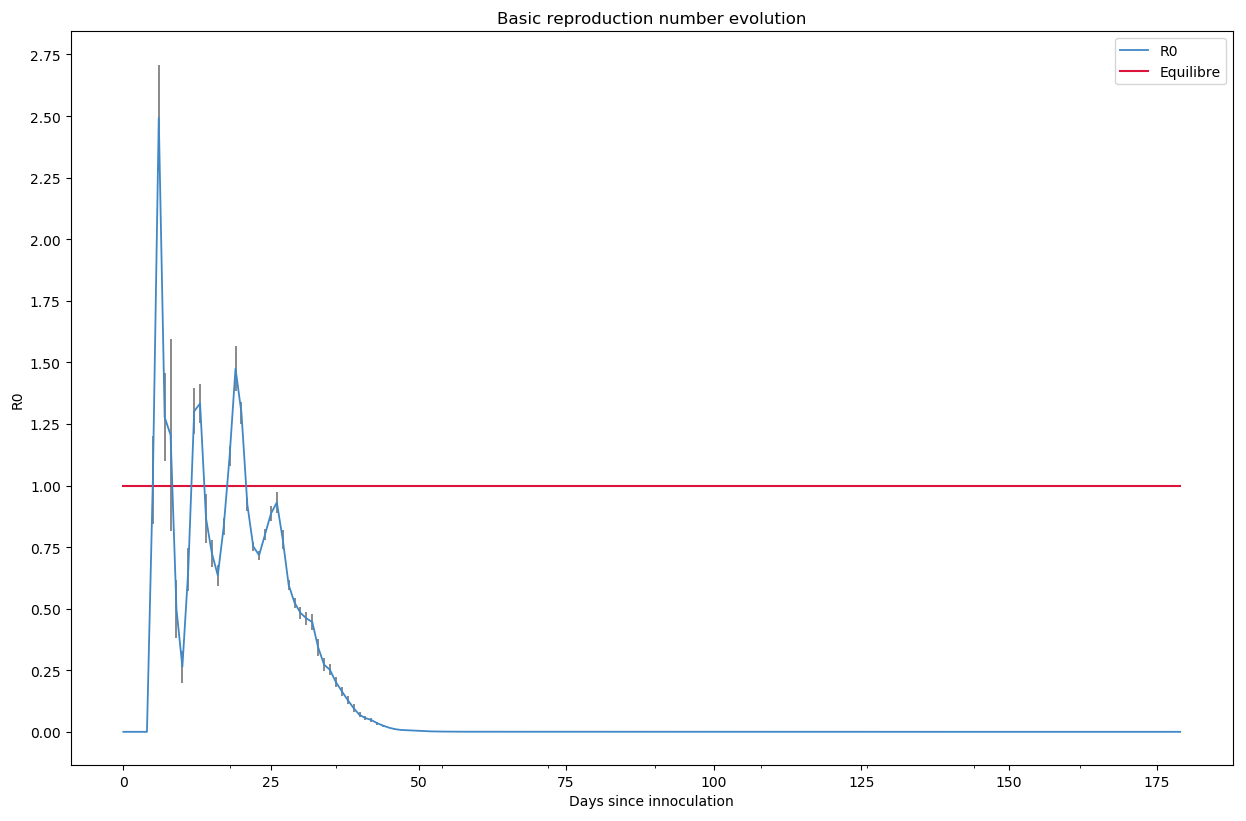
Sur nos 20 simulations, la pandémie connaît en moyenne trois phases quasi exponentielles avec un R0 approchant les 2.75 caractéristique de maladies contagieuses (sans atteindre le R0 de la varicelle qui va jusqu’à 12). J’interprète ces 3 phases comme des périodes de contamination faciles (à la maison par exemple) par opposition à des périodes où il y a une saturation de l’infection (tout le monde est déjà contaminé à la maison et au travail). Puis une ou plusieurs personnes infectées décident d’aller dans une épicerie un peu plus loin (parce qu’il paraît que là-bas il font une meilleure chbakia) ou d’avoir un mauvais comportement (les masques sont réutilisés et on ne se lave pas les mains en rentrant chez soi) et c’est reparti pour un tour.

Pour lancer les simulations précédentes :

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario -1  --draw exa pop summ R0

Quel aurait été le nombre de morts si nous avions suffisamment de lits quelle qu’ait été la situation ? Passons de 85 à 10000 lits par million d’habitants :

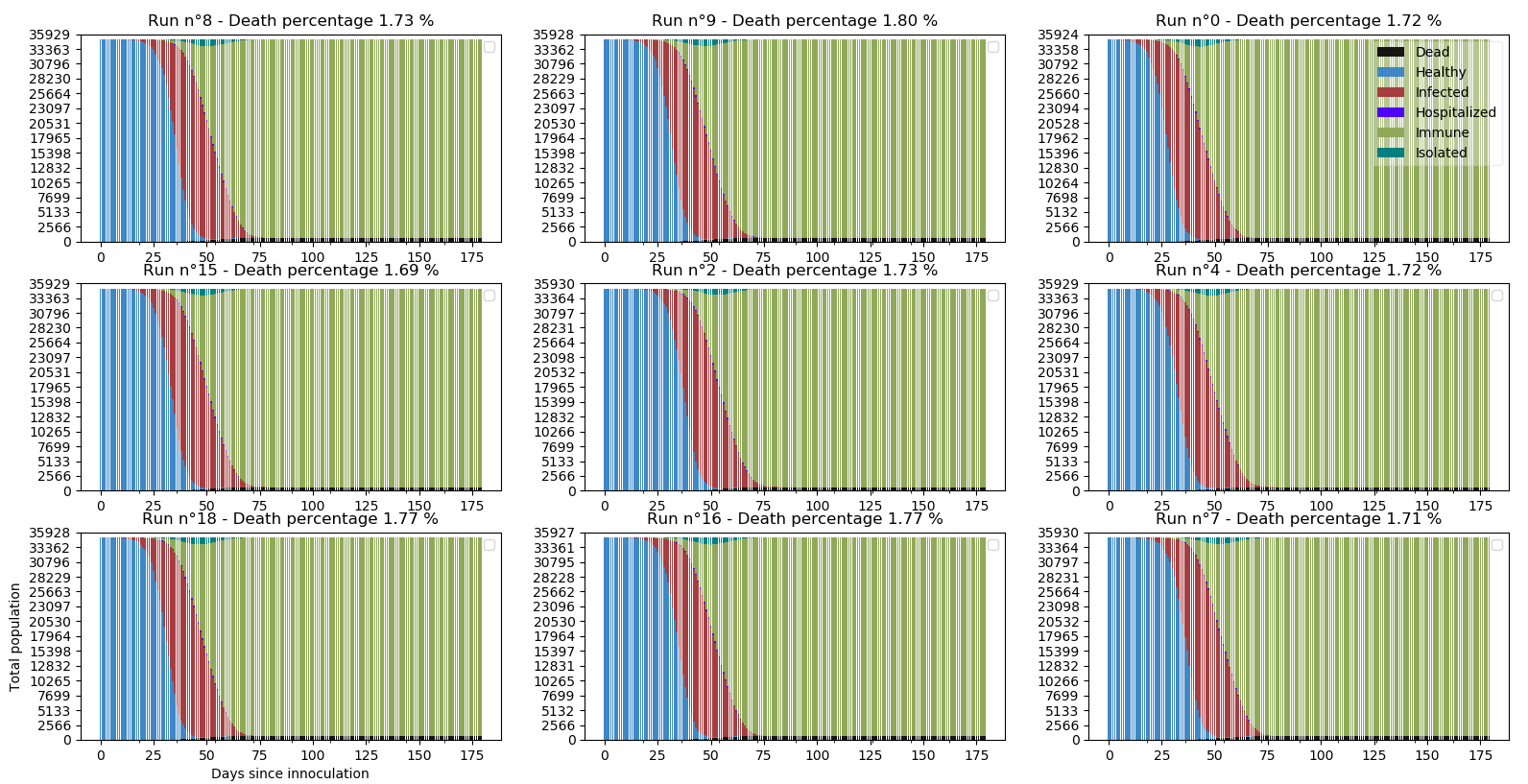
En moyenne 1.73% sur les 9 simulations les plus distinctes soit une différence de 1.2 points avec le scénario de base de saturation des hôpitaux. Notons qu’à l’échelle d’un pays comme le nôtre, 1.2 points de population correspond à 420.000 personnes décédées. Cela donne froid dans le dos.

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario -1 --nbeds-icu 10  --draw exa pop summ R0

Takeaway scénario X

En l’absence de mesure de confinement, l’infection est complètement généralisée, les hôpitaux saturés et de nombreuses personnes mourront sans avoir eu la chance d’une aide médicale. C’est un scénario cruel pour les personnes fragiles infectées durant le pic de saturation des infrastructures de santé.

Revenir à l’index

Scénario 0 : Éradication totale (dit scénario de l’asile psychiatrique)

Le confinement actuel est maintenu indéfiniment. Car on ne sait jamais si le virus est dormant sur une porte de tramway ou un étal de supermarché.

Considérons les paramètres en situation de confinement décrits plus haut. La pandémie risque de durer plus longtemps : Augmentons la durée des simulations à 360 jours.

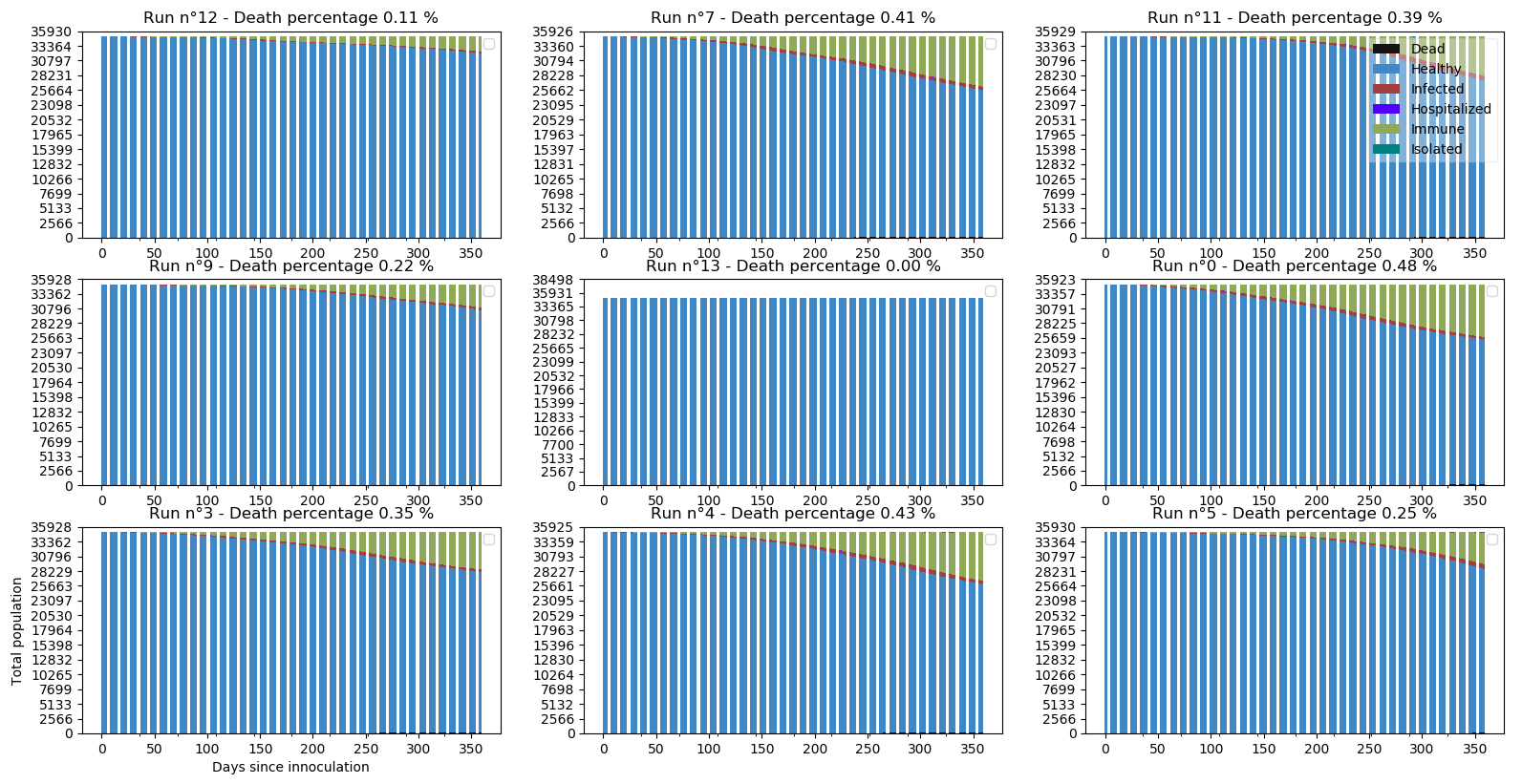
Globalement sur les 9 simulations choisies (parmi 20), la pandémie est fortement retardée sans être tout à fait étouffée. Il est fascinant de constater que celle-ci s’est éteinte sur la simulation n°13, probablement parce que les personnes initialement infectées travaillaient à distance ou vivaient seules. Une pandémie c’est aussi beaucoup de variabilité et donc un lancé de dé au départ (ce qui me fait penser à la Mauritanie qui aurait contenu le Covid-19).

Comment a réagit le système hospitalier ?

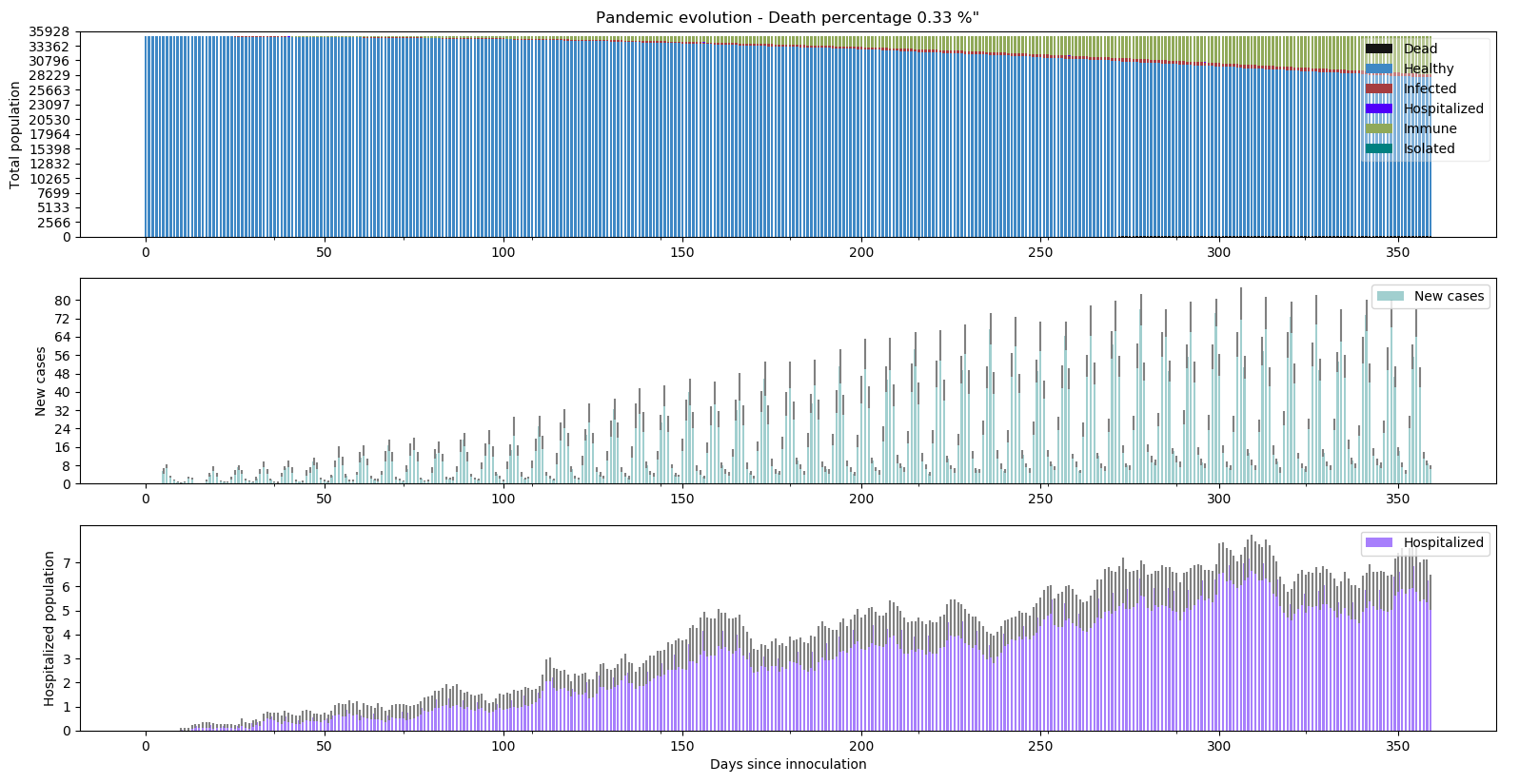
Plutôt bien puisque le niveau d’hospitalisation est au maximum de la capacité de lits en soins intensifs sans la dépasser vraiment. Le confinement fonctionne puisqu’il permet de juguler le nombre de nouveaux cas (maximum de 70 versus 2300 dans le scénario X) et la surcharge des hôpitaux (5 versus 300 dans le scénario X).

Il est encore plus intéressant de constater que dans certaines simulations (par exemple les n°5, n°9 et n°12), le déclenchement de la pandémie est retardé de dizaines de jours ce qui peut laisser du temps aux autorités de mieux se préparer.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.02 --draw exa pop summ R0

Mais comment évolue la situation au-delà ? Faisons l’expérience d’aller chercher le devenir de la pandémie au bout de 900 jours (soit quasiment 3 ans) :

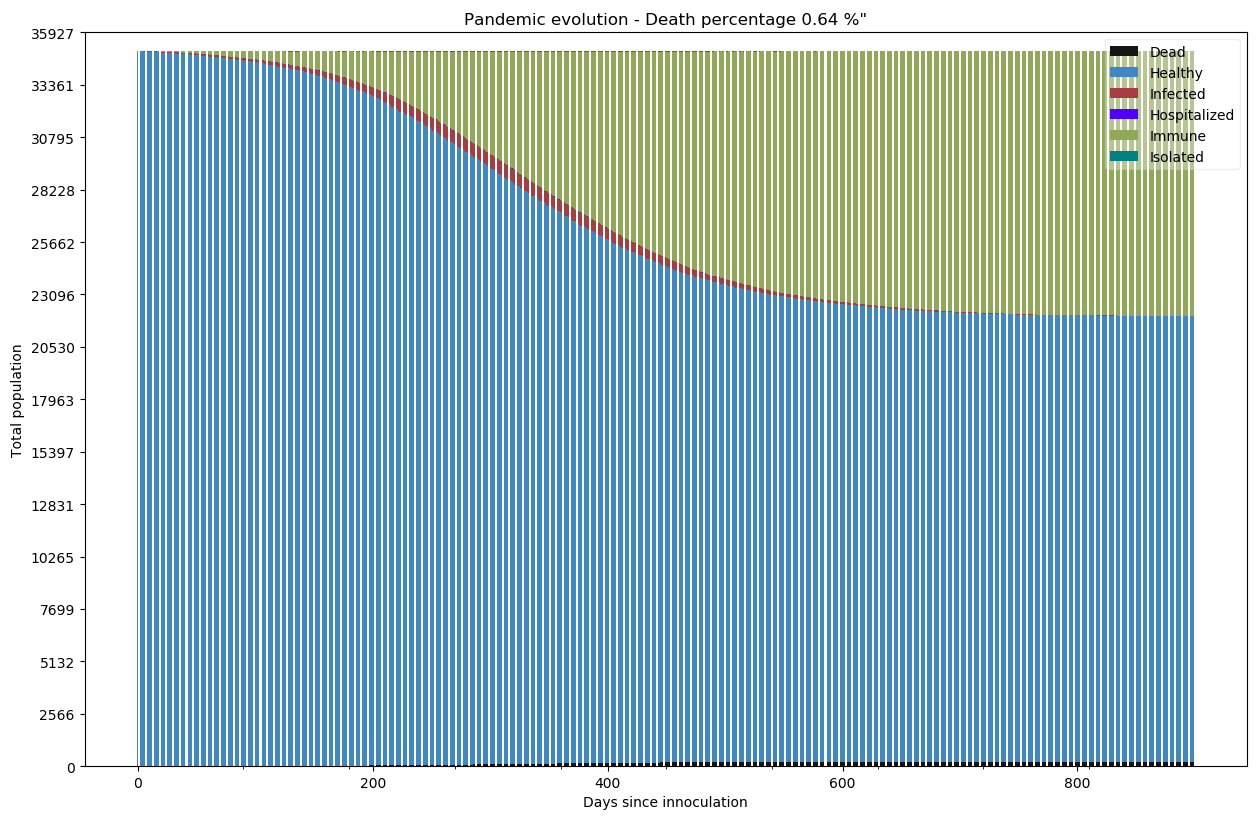
L’immunité collective semble atteinte avec un pourcentage non négligeable de la population infectée (ici près de 40% d’infectés). Mon interprétation est que le télétravail a clairement protégé car il s’applique à une part importante de la population (98% ici) même si le déplacement dans les épiceries reste un vecteur de risque important. L’immunité d’une part importante de la population combinée à un confinement modéré a éteint la pandémie en 3 ans.

Quand on regarde l’évolution du nombre de nouveaux cas quotidien :

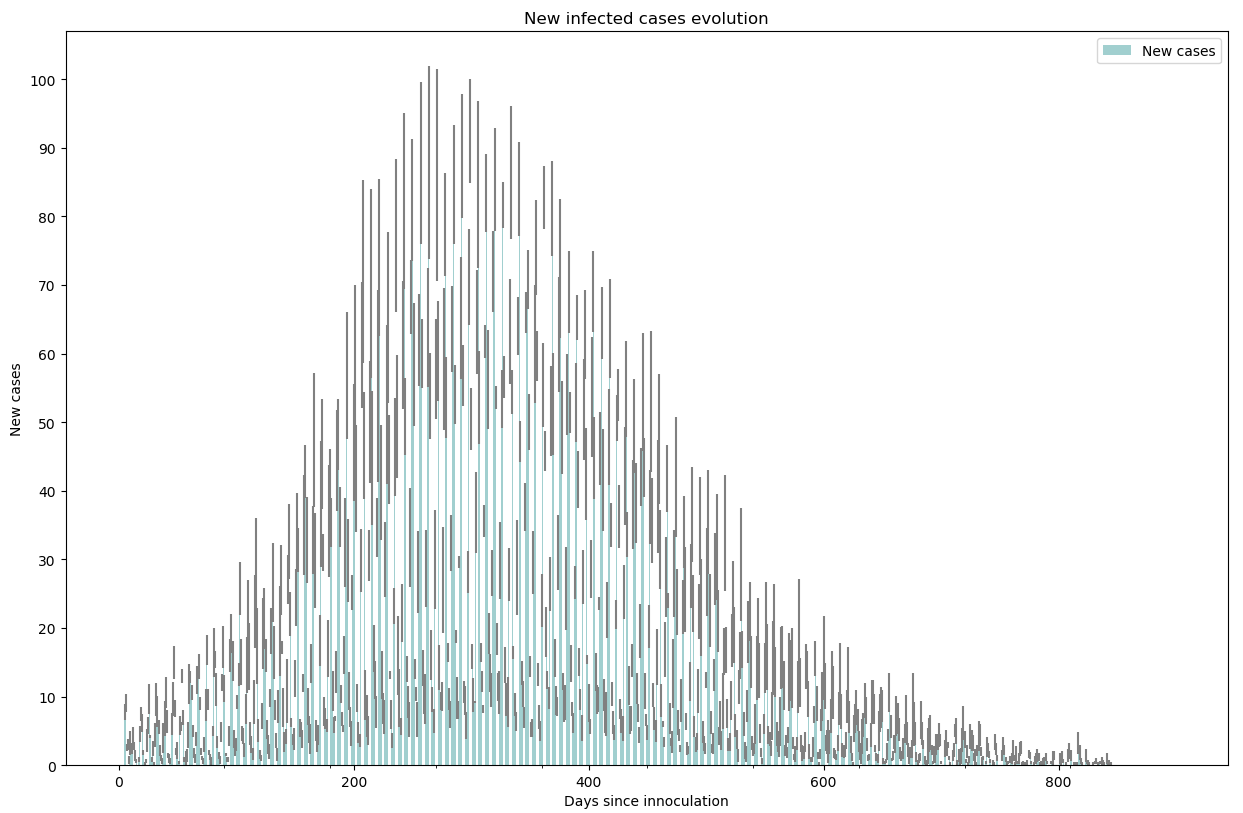
Les barres grises correspondent à la variabilité (ou écart standard) sur les simulations que nous lançons. Le pic de nouveaux infectés ne dépasse pas les 75 personnes en moyenne. Et diminue très lentement.

python -m scenario.run --nrun 5  --nday 900 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.02 --draw pop new

Confinement strict ?

Le confinement fonctionne mais 3 ans c’est beaucoup trop long. Et si nous mettions en place un confinement strict (mais pas impossible) qui se traduirait par une probabilité de contagion à l’épicerie extrêmement faible (0.1%) (le moqaddem vient vous ramener un panier désinfecté de nourriture devant le pas de votre porte tous les 3 jours) tout en maintenant les 5% de travailleurs sur place (lançons cette fois-ci 40 simulations sur une durée plus courte de 90 jours) :

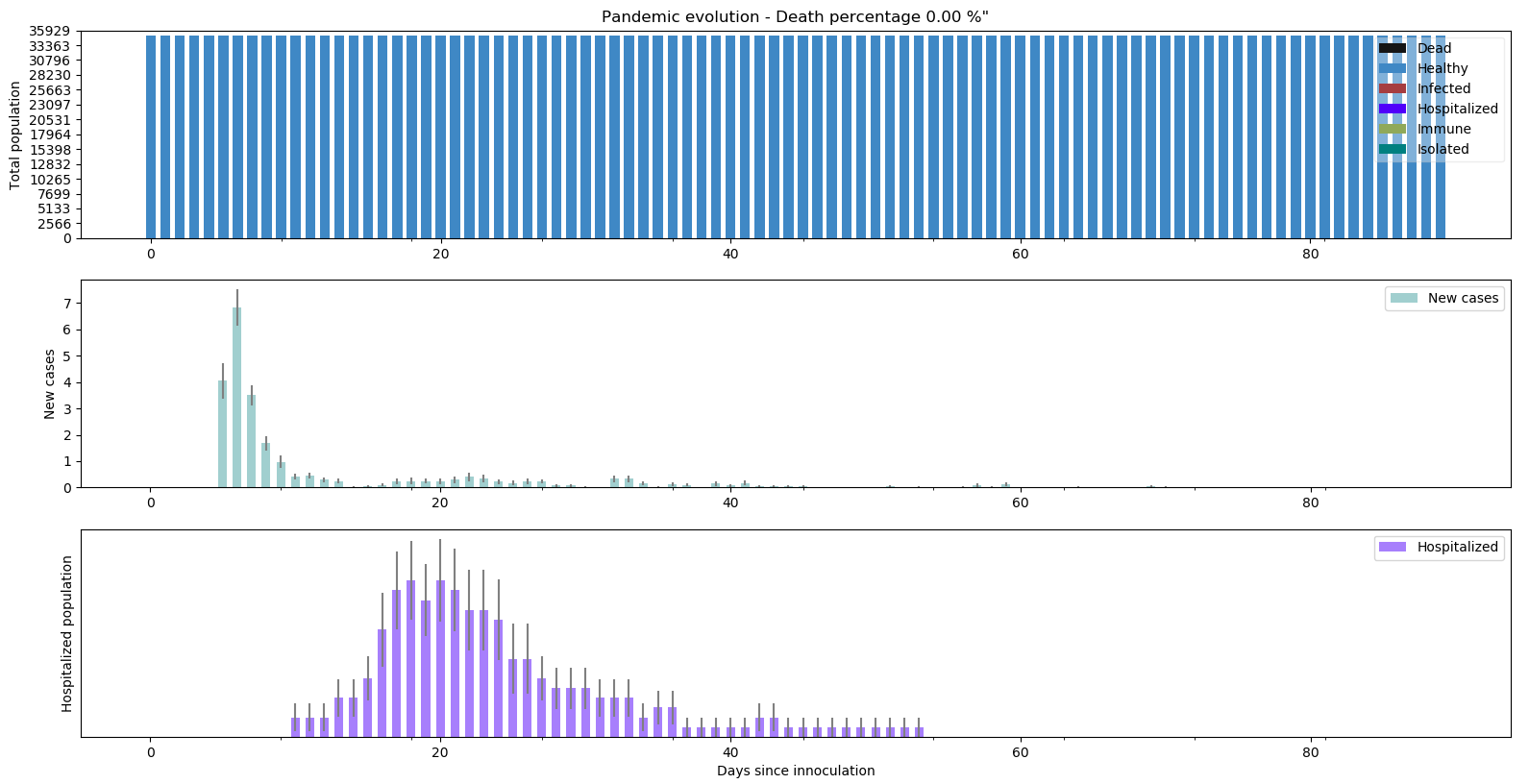
La pandémie est instantanément anéantie. Et ce même si le dernier cas de nouvelle infection peut subsister jusqu’au 60ème jour.

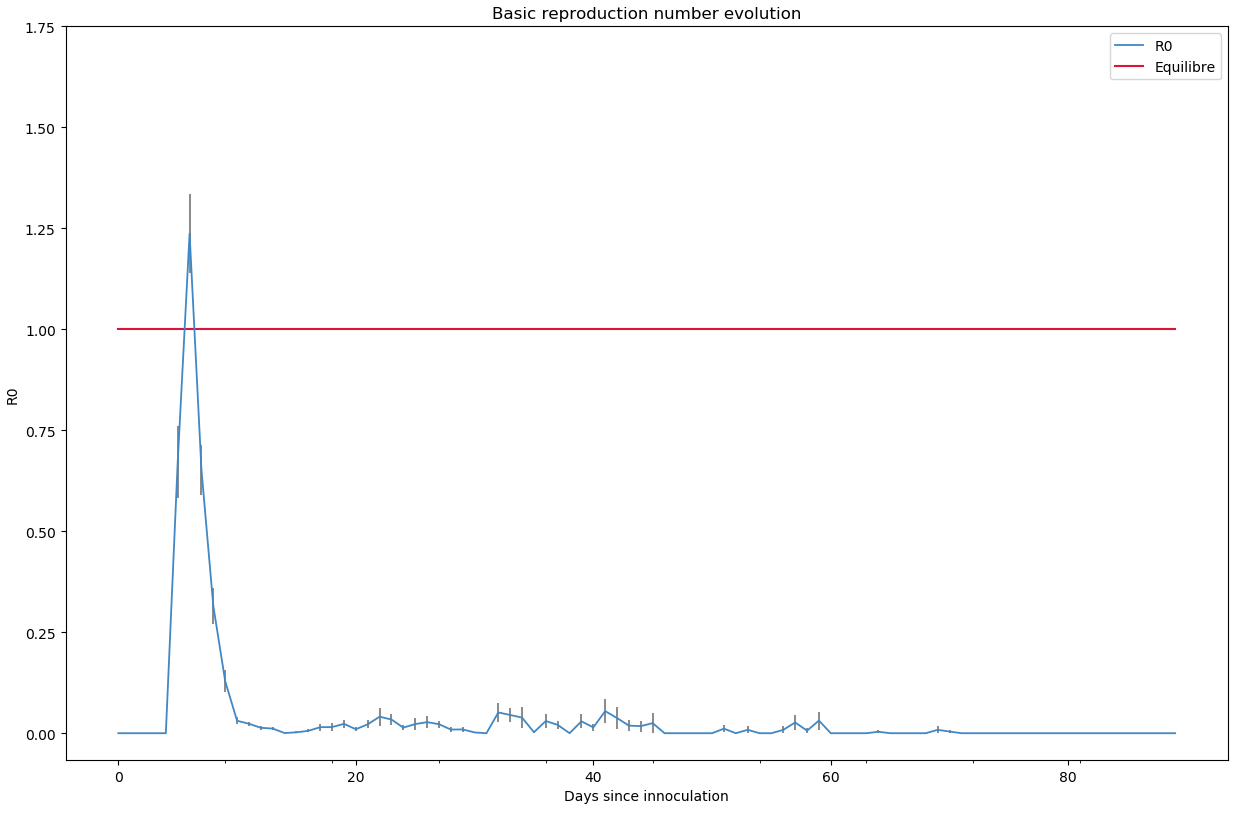
L’évolution du coefficient R0 montre bien qu’une fois les passé les premiers jours (les 5 premiers infectés contaminent leur entourage proche - famille et travail lorsque c’est le cas), le R0 tombe naturellement à quasiment 0.

python -m scenario.run --nrun 40  --nday 90 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.001  --draw exa pop summ R0

Pour rendre la situation plus réaliste (et plus proche de ce que nous vivons au Maroc), nous partirons dans les scénarios suivants sur le même confinement strict en corsant un peu le point de départ : 50 personnes initialement infectées.

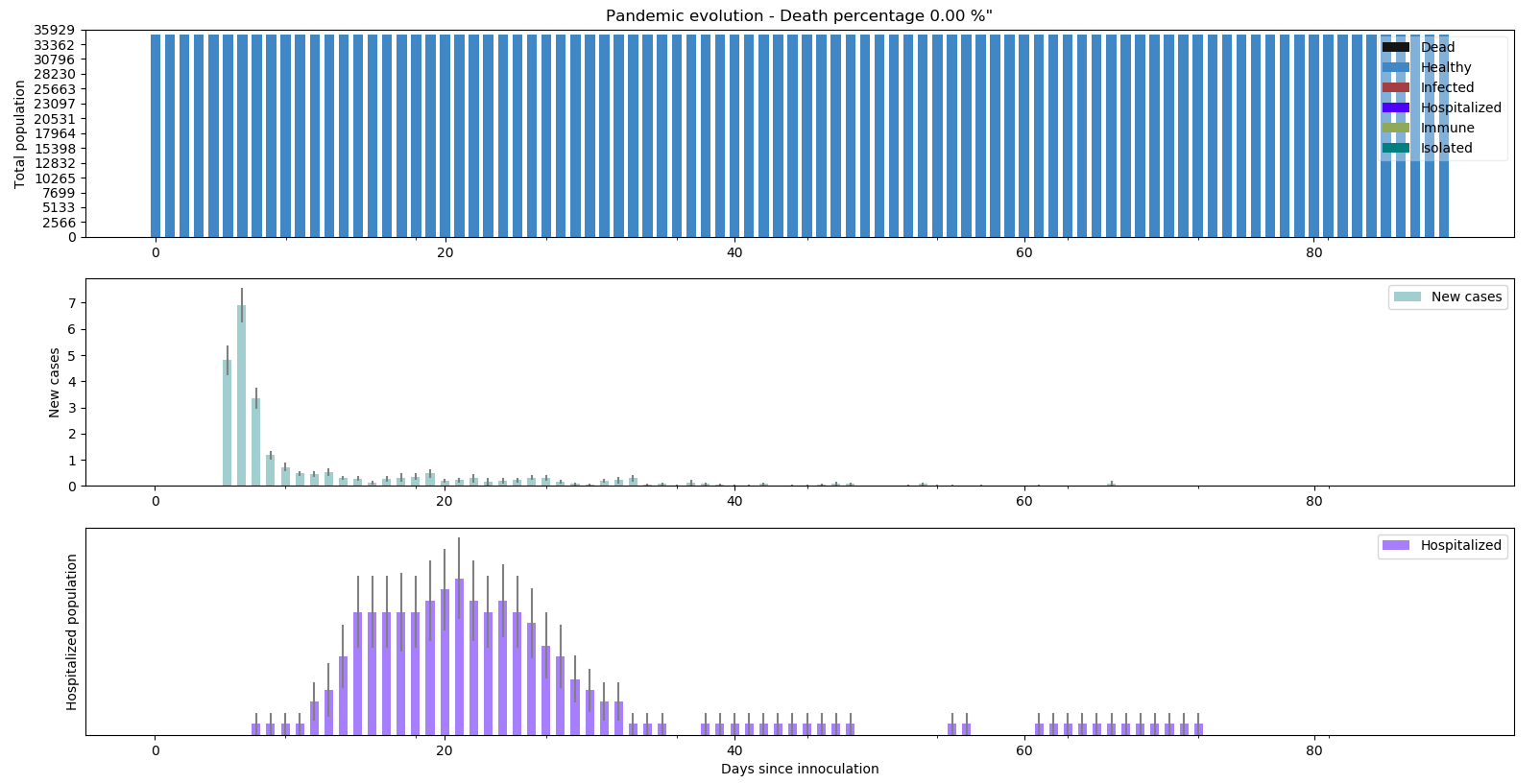
Pas de surprise, le confinement strict est efficace tant qu’il est prolongé indéfiniment.

python -m scenario.run --nrun 40  --nday 90 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.001 --inn 50  --draw exa pop summ R0

Takeaway scénario 0

L’épidémie peut donc se prolonger plusieurs année dans certaines simulations. Mais confiner 35.000 individus pour quelques dizaines de nouveaux cas quotidiens paraît disproportionné. Un confinement strict jugule fortement l’épidémie. Combiné à un contrôle proactif des autorités, le virus pourrait rapidement disparaître. Mais ce scénario semble fort peu probable en raison de sa durée insoutenable pour la société et l’économie.

Revenir à l’index

Scénario 1 : Éradication totale puis retour au bon vieux temps (dit scénario sbro m3ana)

Le confinement infini n’est pas réaliste. Par conséquent, nous allons maintenir le confinement strict défini précédemment jusqu’à extinction totale du nombre de nouveaux cas et étendu un certain nombre de jours après. Puis le déconfinement est progressif : les frontières restent fermées mais la vie quotidienne peut reprendre un cours normal en espérant qu’il n’y ait pas de foyers caché…

Reprenons le paramétrage en situation de confinement strict avec un nombre personnes initialement infectées à 50, mais cette fois-ci, à chaque fois que 14 jours sont passés sans nouveau cas, tous les paramètres de contagion sont passés à la racine dont augmentés (c’est à dire que 0.01 de probabilité de contagion devient 0.1) et les paramètres décroissants en dureté de confinement passés au carré (98% de télétravailleurs devient 96%). On pourrait appliquer d’autres fonctions mais celles-ci font l’affaire puisque les probabilités restent dans [0,1] et sont monotones.

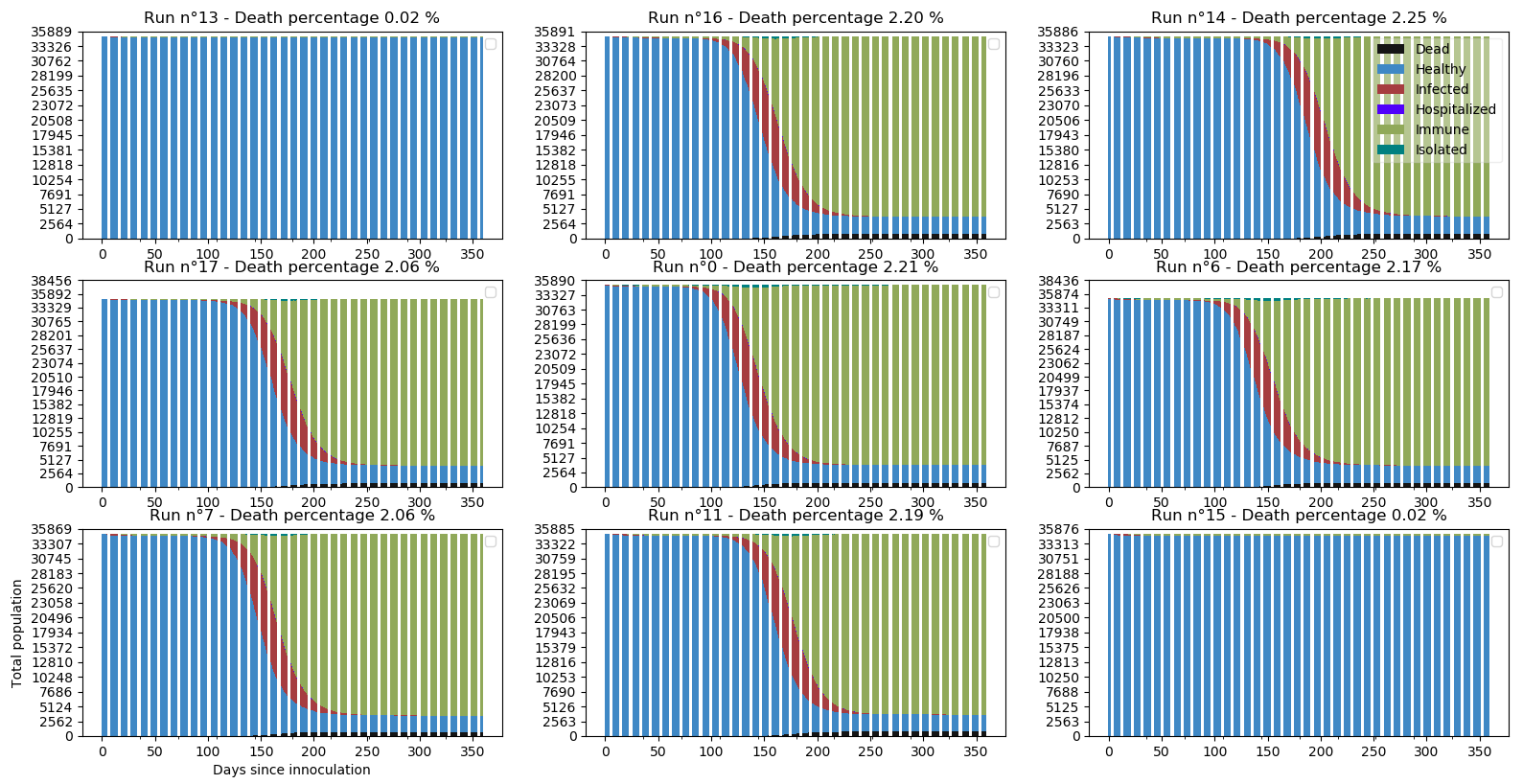
Sur les 9 simulations les plus distinctes, 7 connaissent un scénario catastrophe : le déconfinement a été réalisé trop tôt malgré la période de sûreté et la progression de la pandémie redevient exponentielle. Pour les simulations n°13 et n°15, attendre 14 jours a été suffisant. Dans cette configuration, le déconfinement arrive en moyenne après 56.10 jours (avec un pic à 82 jours pour une des simulations) ce qui est relativement honnête et acceptable pour la population. Mais visiblement insuffisant en moyenne pour le contrôle de la pandémie.

Si on observe le résumé moyen des simulations, nous avons 0.80% de décès avec une variabilité importante comme nous venons de le voir précédemment :

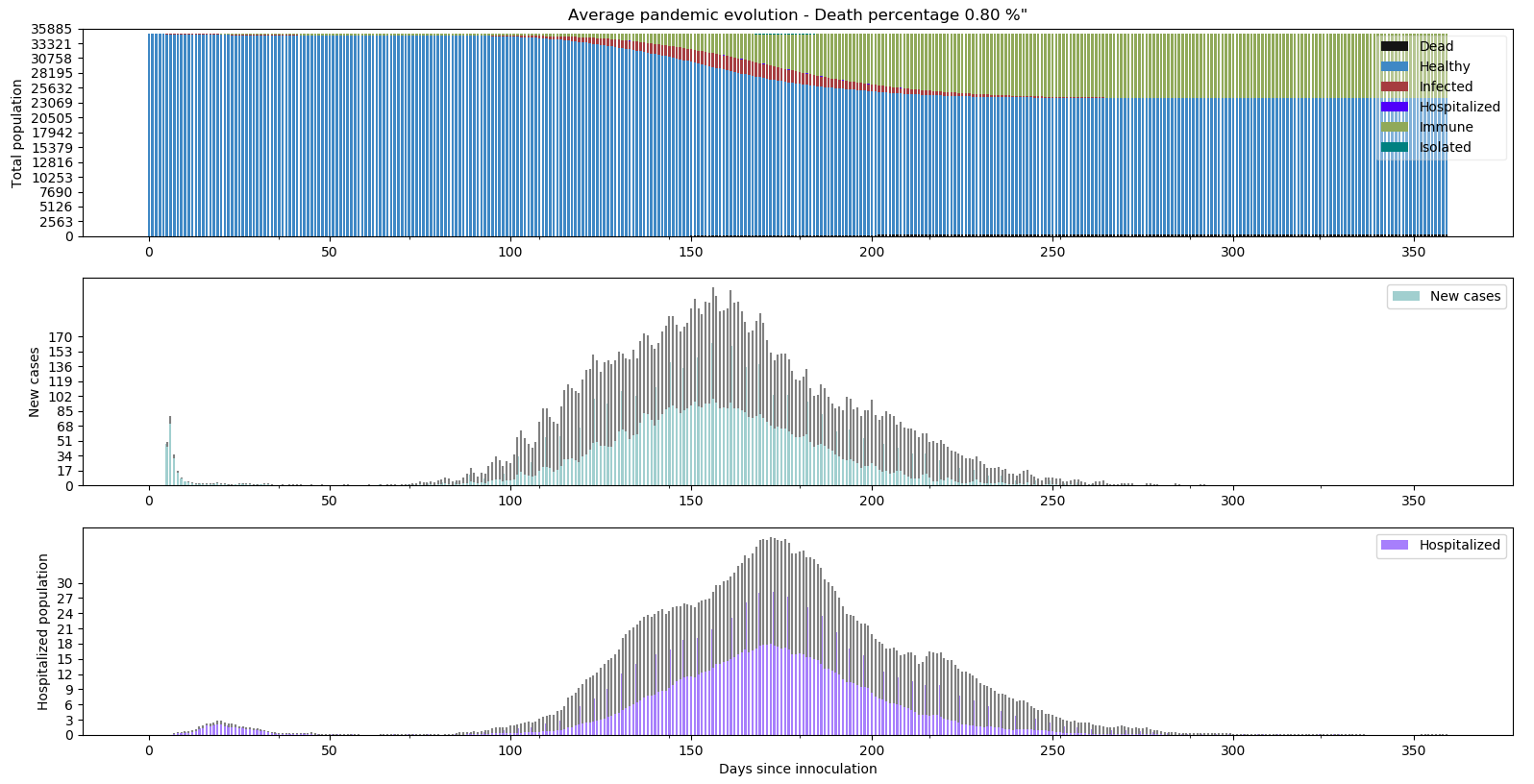
Les hospitalisations en violet atteignent tout de même des niveaux importants (24 lits), bien au delà des 4 lits de capacité maximum.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 1 --extra 14 --draw exa pop summ lock hos new R0

Regardons ce que ça donne en attendant cette fois-ci 21 jours après la dernière occurrence de nouvelle infection :

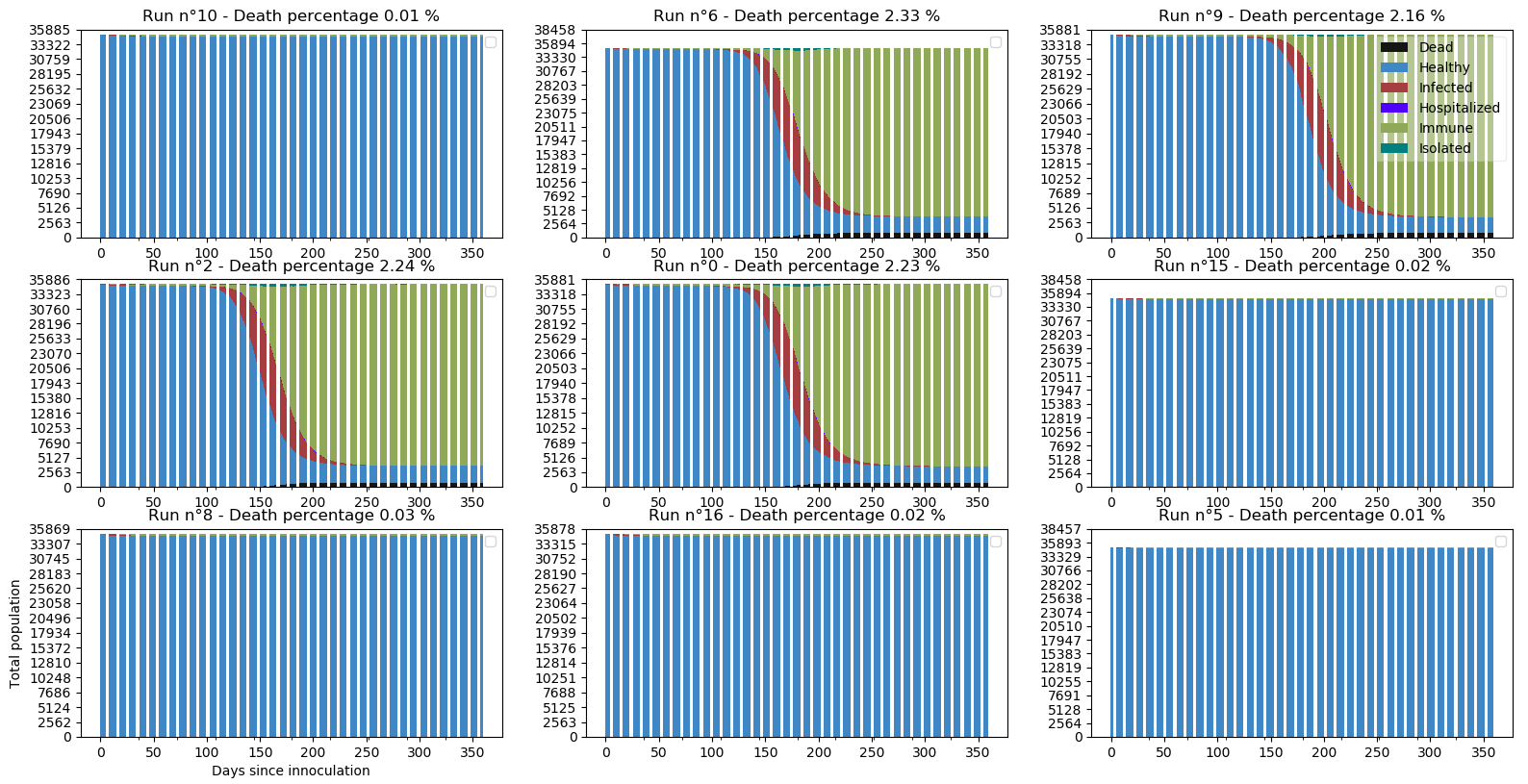
Attendre 3 semaines est bien plus encourageant. Sur les 9 simulations remarquables, seules 4 ont viré au cauchemar au bout d’une centaine de jours tandis que les autres ont permis une maîtrise de la pandémie. Dans cette configuration, le déconfinement intervient en moyenne après 66.48 jours.

Mesurons la dureté moyenne du confinement par une fonction des probabilités de contagion, du taux de télétravail et de la probabilité d’aller à l’épicerie la plus proche. Plus la valeur est élevée et plus le confinement est sévère.

Si on observe la variation de la dureté du confinement :

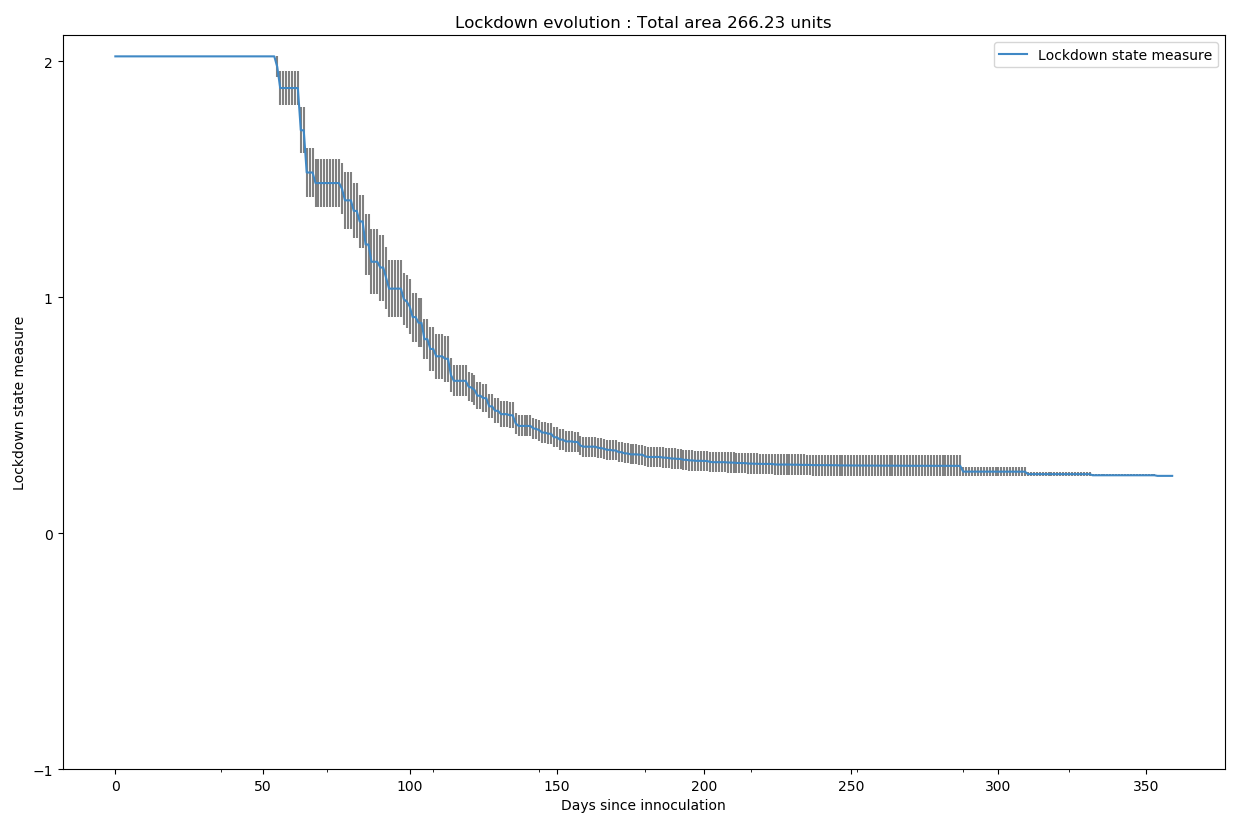
Tel qu’espéré, le confinement diminue au fur et à mesure au bout de la cinquantaine de jours. L’intégrale du confinement correspond à la quantité de douleur sociétale et économique endurée. Dans ce scénario, nous avons 266 unités (contre 307 unités en attendant 14 jours).

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 1 --extra 21 --draw exa pop summ lock hos new R0

Vérifions enfin qu’en définissant une période de sûreté de 28 jours, aucune de nos simulation ne voit sa situation échapper à tout contrôle :

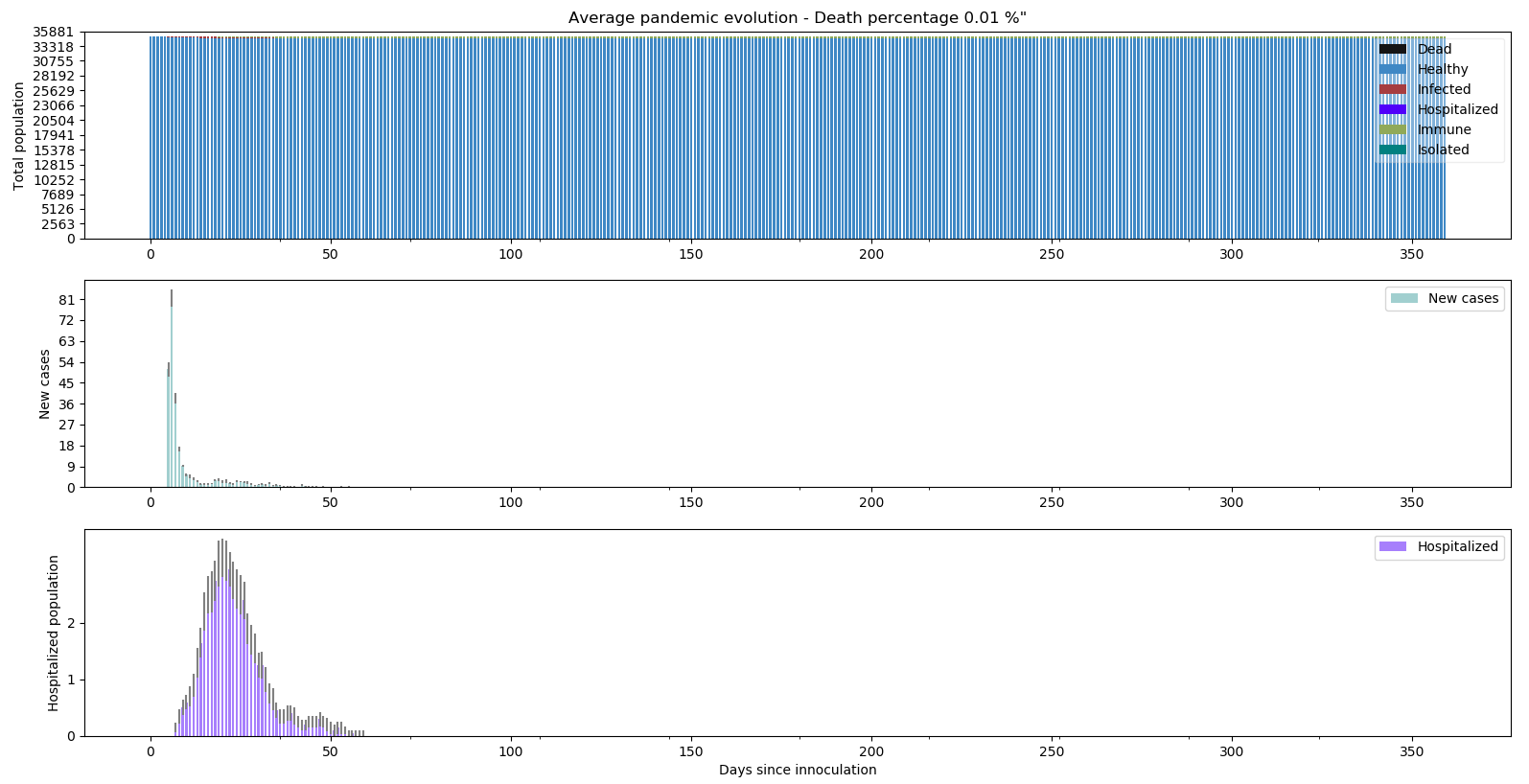
On constate bien que la pandémie est parfaitement jugulée. Le relâchement se fait en moyenne au bout de 75.33 jours avec un pic de 105 jours pour l’une des simulations.

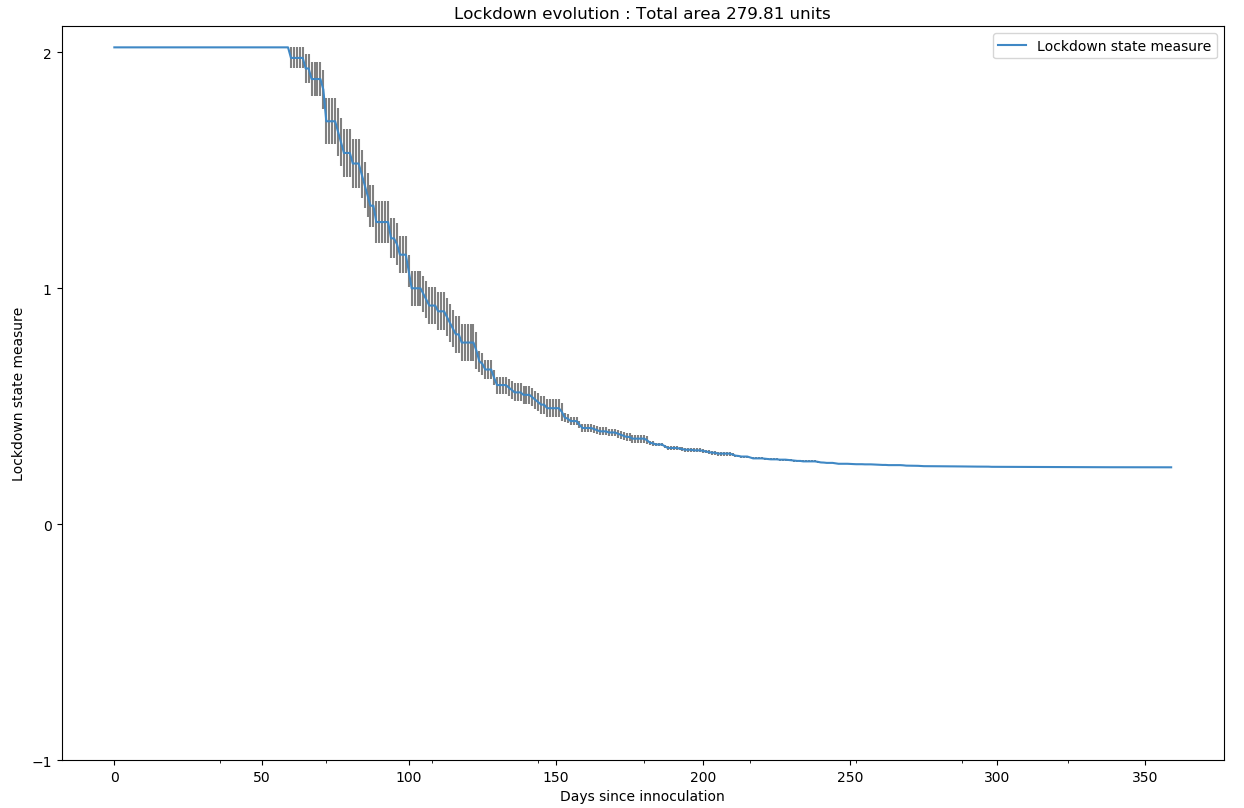
Il est logique de constater que la dureté du confinement pour 28 jours d’attente est de 279 unités, soit 13 unités supplémentaires par rapport au scénario à 21 jours d’attente (266 unités). Attendre plus longtemps avant de déconfiner augmente la “quantité totale de confinement”.

Ce qui est par contre plus étonnant de remarquer, c’est que le premier scénario à 14 jours d’attente a un nombre d’unités plus élevé que les deux derniers scénarios. Déconfiner plus vite pour soulager la population et l’économie s’avère contre-productif sur le long terme. Attendre plus longtemps avant de déconfiner, c’est d’une part s’assurer contre le risque d’une rechute pandémique, et d’autre part avoir plus de libertés globalement durant le cours de la pandémie. Sbro m3ana.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 1 --extra 28 --draw exa pop summ lock hos new R0

Takeaway scénario 1

Le déconfinement progressif paraît être l’option idéale pour contrôler la propagation du virus sans asphyxier la société. Dans notre jeu de paramètres, une durée de 21 jours d’attente après la dernière nouvelle infection a donné des résultats encourageants qui paraissent à peu près optimaux. Attendre seulement 14 jours semble bien trop risqué. Mais 3 semaines c’est beaucoup trop long. Il faudrait idéalement déconfiner rapidement par exemple après 7 jours et pouvoir ajuster au besoin selon l’évolution de la situation. Peut-on avoir plus de souplesse et déconfiner/reconfiner en fonction de l’évolution de la propagation ?

Revenir à l’index

Scénario 2 : Le risque modulé (dit scénario du yo-yo)

Le modèle du scénario 1 a permis d’extraire une variable intéressante : le nombre de jours avant le début du déconfinement. 21 jours a semblé un sweet spot pour un déconfinement responsable. Mais ce sont 21 jours après la dernière infection déclarée et celle-ci peut tarder. En moyenne avec notre scénario 1 à 21 jours d’attente, il a fallu attendre 66 jours pour la dernière occurence d’infection. Une population peut-elle tenir aussi longtemps sans incivilités ^[15] ?

Si on y réfléchit un peu plus, le vrai trade-off à aller chercher est bien entre le niveau de saturation des hôpitaux ^[10] et le niveau de confinement de la population. Confiner c’est soulager le système sanitaire, mais c’est aussi fragiliser l’économie ^[16] et s’exposer à un mécontentement populaire au mieux, à des manifestations et révoltes au pire ^[14].

Le scénario 1 n’est donc à première vue pas réalisable et un déconfinement temporaire doit survenir pour relâcher la pression. A quel moment celui-ci peut-il être réalisé et pendant combien de temps ? Suivant quelle périodicité ?

Testons un nouveau scénario :

• Dès qu’il n’y a plus de nouveaux cas déclarés, le relâchement est acté au bout de 7 jours d’attente (toujours à travers la procédure citée plus haut) comme dans le scénario 1
• Mais dès que la saturation des hôpitaux est atteinte, le confinement est resserré (à travers vous l’avez deviné les fonctions inverses de la procédure de déconfinement)
• Deux changements successifs de configuration de confinement (relâchement ou resserrement) ne peuvent arriver qu’au minimum 7 jours d’intervalle (en raison de l’inertie sociale organisationnelle de tels changement)

Sachant que tuer la pandémie nécessiterait trop de temps et trop de confinement, le but assumé est double :

1. Maintenir les hôpitaux à un niveau de saturation optimal (1 à 2 fois le maximum soit jamais plus de 4 à 8 lits occupés) afin de garder des taux de mortalité normaux
2. Obtenir la quantité totale d’unités de confinement minimale

Et tenir le plus longtemps possible jusqu’à extinction de la pandémie par chance ou immunité globale. Peut-on faire cela ?

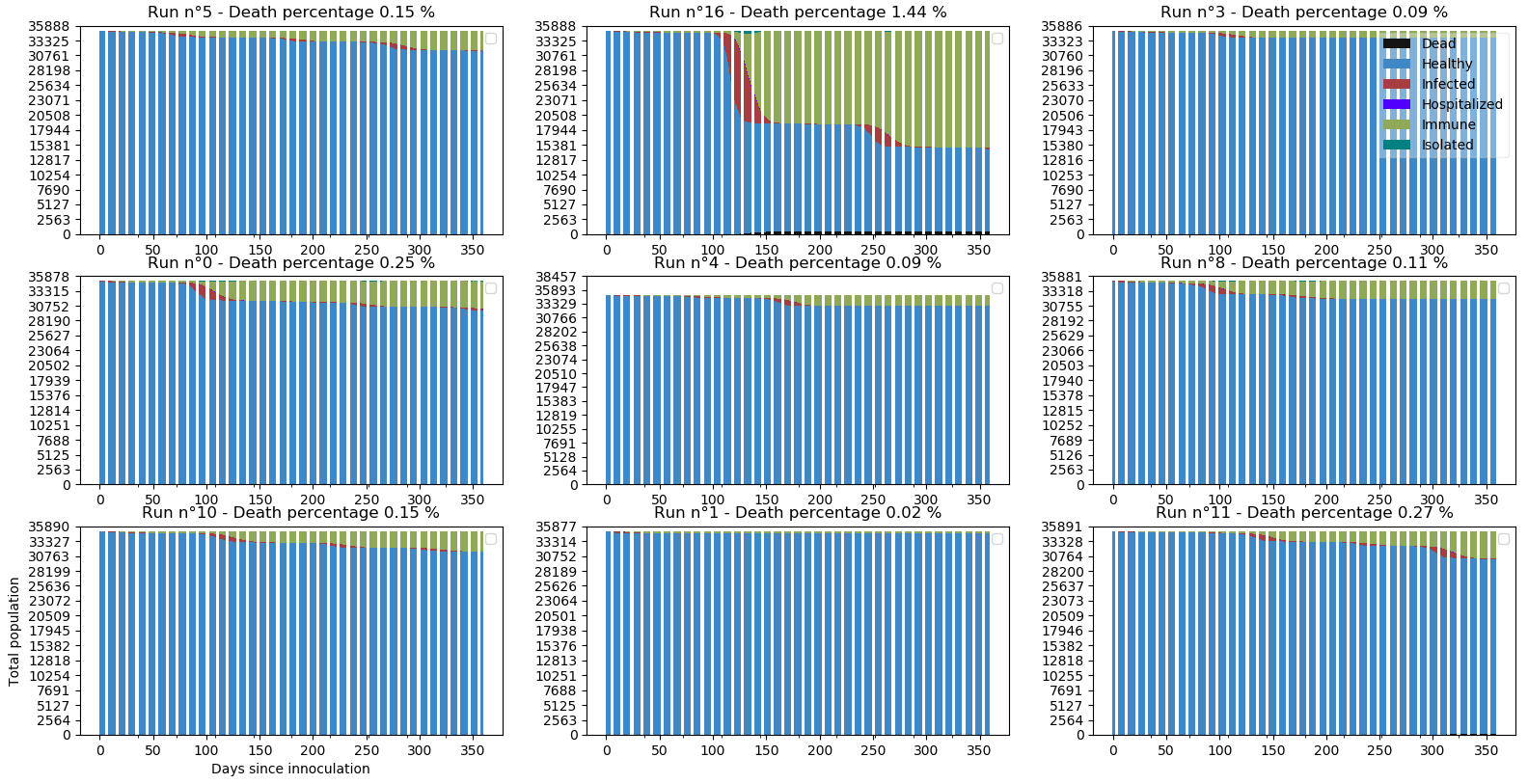
Voilà qui est intéressant. Le déconfinement de la simulation n°16 n’a pas pu être rattrapé par les resserrements de confinements et la situation a dégénéré (1.44% de morts). Mais la situation est maîtrisée dans la plupart des simulations.

En moyenne, le graphe ci-dessous montre 0.19% de mortalité et une courbe d’hospitalisation (violet) qui fait des vagues.

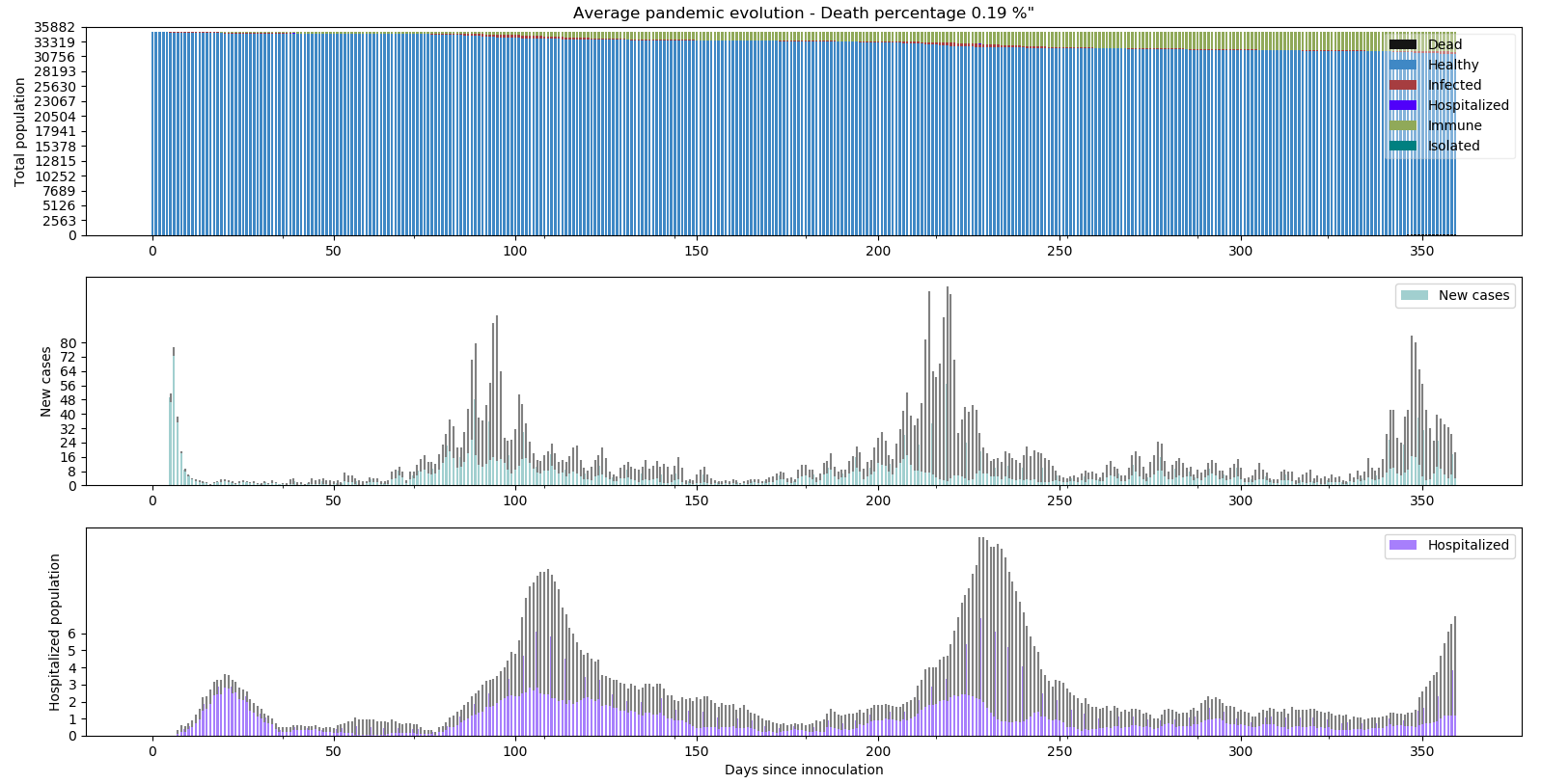
Les chiffres au premier abord paraissent satisfaisant mais a-t-on suffisamment déconfiné ?

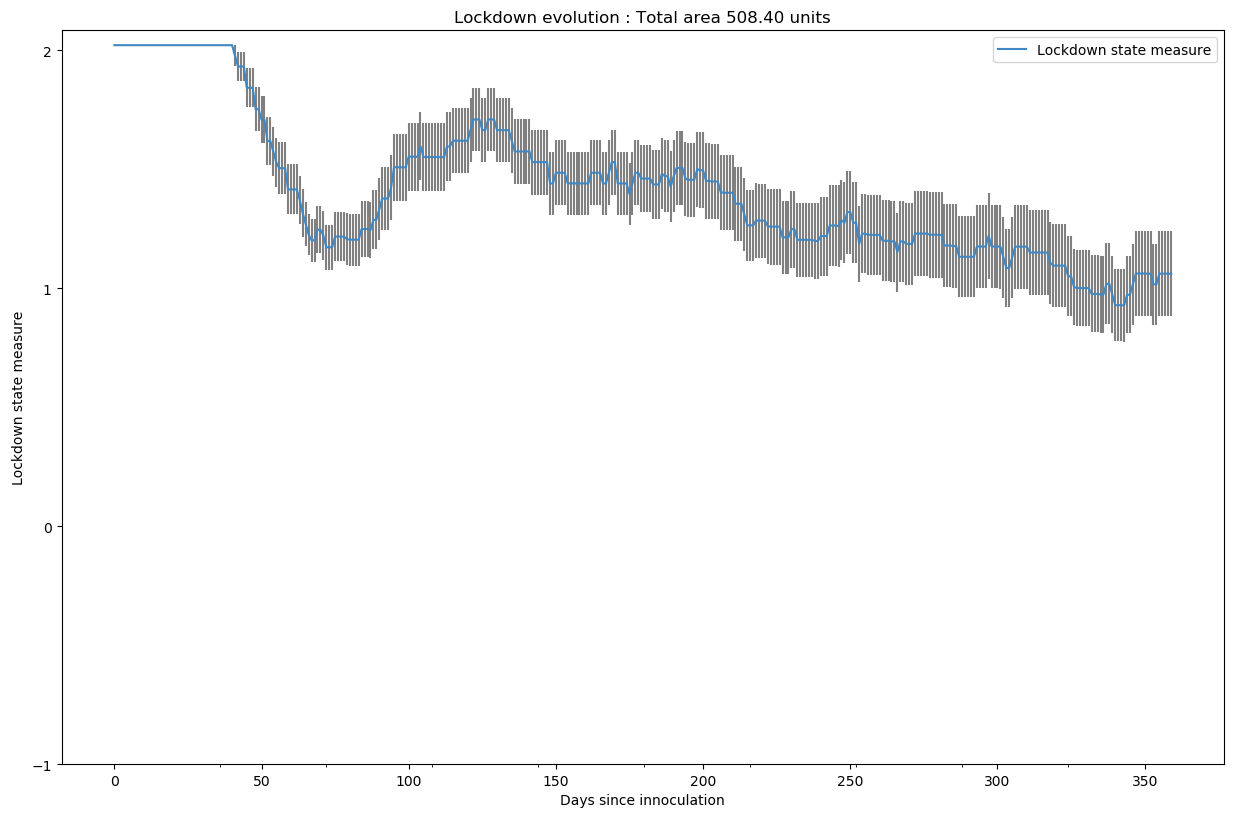
508 unités de confinement sur les 360 jours, c’est bien au-dessus de nos variantes du scénario 1 (200 à 300 unités de confinement).

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 2 --extra 7 1 2  --draw exa pop summ lock hos new R0

Essayons de chercher à atteindre une valeur la plus faible possible sans trop retarder le déconfinement :

Le relâchement sera cette fois-ci acté au bout de 14 jours :

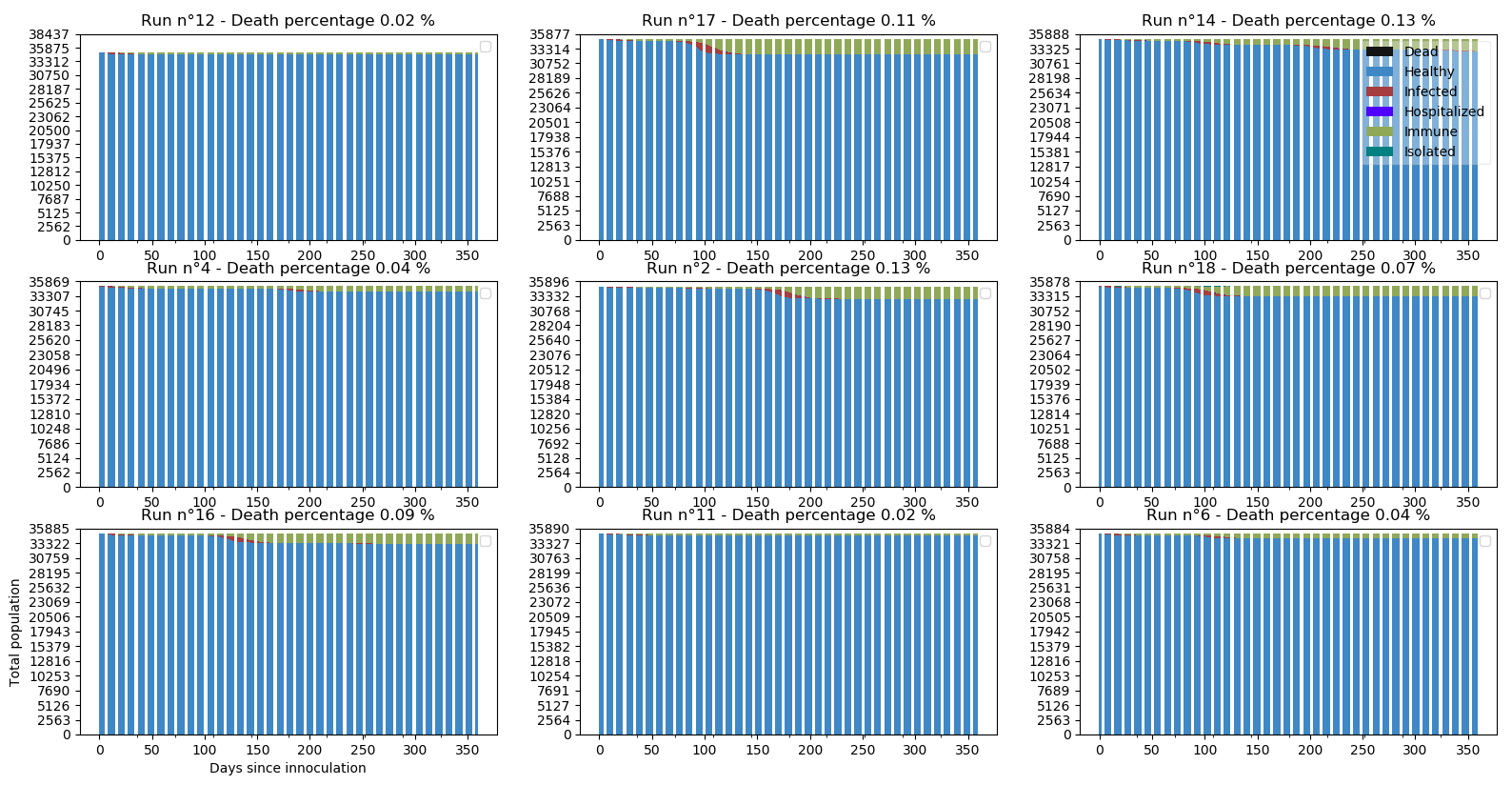
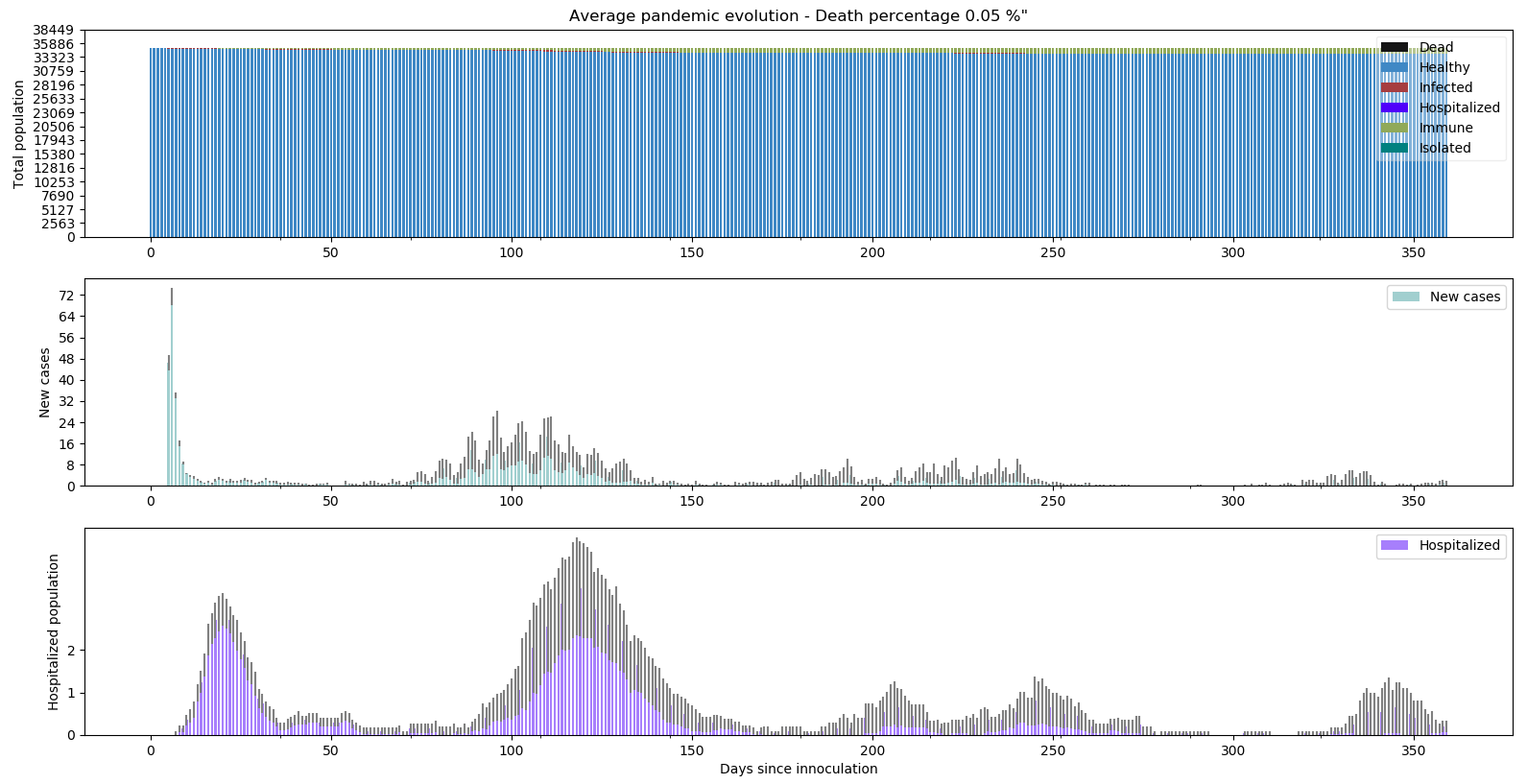
Aucune simulation catastrophe cette fois-ci. Le niveau d’hospitalisation reste modéré sans même atteindre en moyenne la capacité maximum.

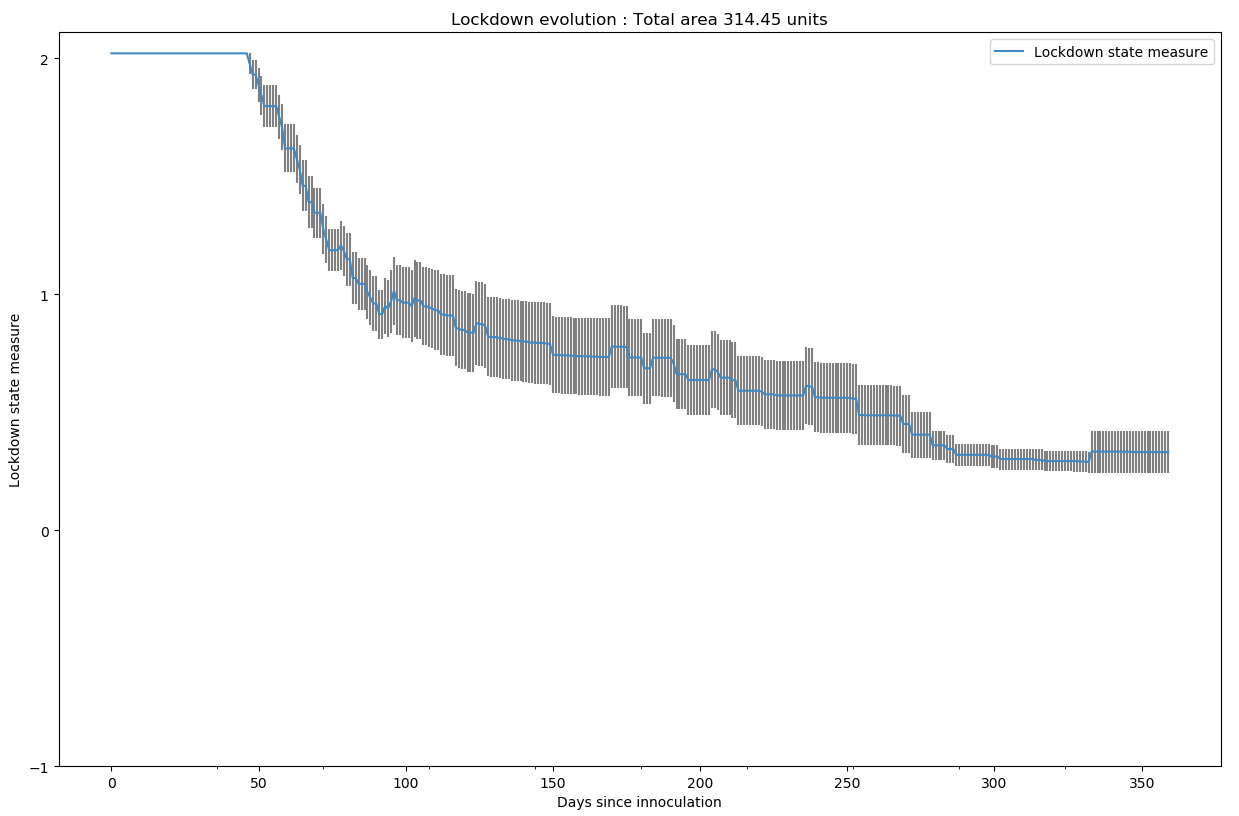
Quant au niveau de confinement, nous avons un excellent 314 unités de l’ordre de grandeur. Lorsque nous analysons la courbe finement, il y a des ajustements de type resserrement fréquents entre 50 et 100 jours qui permettent de gérer des situations critiques.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 2 --extra 14 1 2  --draw exa pop summ lock hos new R0

Takeaway scénario 2

Un déconfinement modulé adaptatif paraît être une solution intelligente pour déconfiner rapidement et pouvoir ajuster en cas de réactivation de la pandémie. Peut être qu’attendre 28 jours après le dernier cas et tout déconfiner d’une traite est acceptable et auquel cas le scénario 1 reste possible. Mais nous illustrons ici qu’un déconfinement à seulement 14 jours du dernier nouveau cas associé à la possibilité d’ajuster est un bon compromis sociétal et économique.

Revenir à l’index

Scénario 3 : L’immunité collective (dit scénario de la mitigation)

La fameuse idée proposée par les britanniques et suédois était d’aboutir rapidement à l’immunité collective (atteinte en mai en Suède d’après un officiel ? ) de la manière la plus efficiente possible à travers un confinement très limité combiné à une prise de conscience citoyenne irréprochable. Cette idée est séduisante mais nécessite un changement spontanée des comportements (ce qui est le cas en Suède) et un système de santé robuste. Comment se traduit-elle dans la modélisation proposée ?

Concernant la capacité hospitalière, nous allons la rendre infinie afin de ne pas impacter les tables de mortalité. Après tout, un pays qui se lance dans une immunité collective doit avoir confiance en son système de santé.

De plus, autorisons la population à aller travailler en repassant à 58% de personnes en télétravail et uniquement 30% des individus qui vont à l’épicerie la plus proche. Par contre, nous allons considérer des probabilités de contagion strictes : 1% de contagion au travail et dans les transports publics, 0.1% dans les épiceries et toujours 50% dans les foyers.

Nous avions déjà constaté qu’avec la première partie de ces paramètres, la pandémie fait un ravage. Mais nous avions aussi vu qu’avec la deuxième partie de ces paramètres (probabilités de propagation de confinement strict), le virus et très vite maîtrisé au bout d’une cinquantaine de jours. Comment évoluera l’épidémie avec la combinaison de ces deux facteurs ?

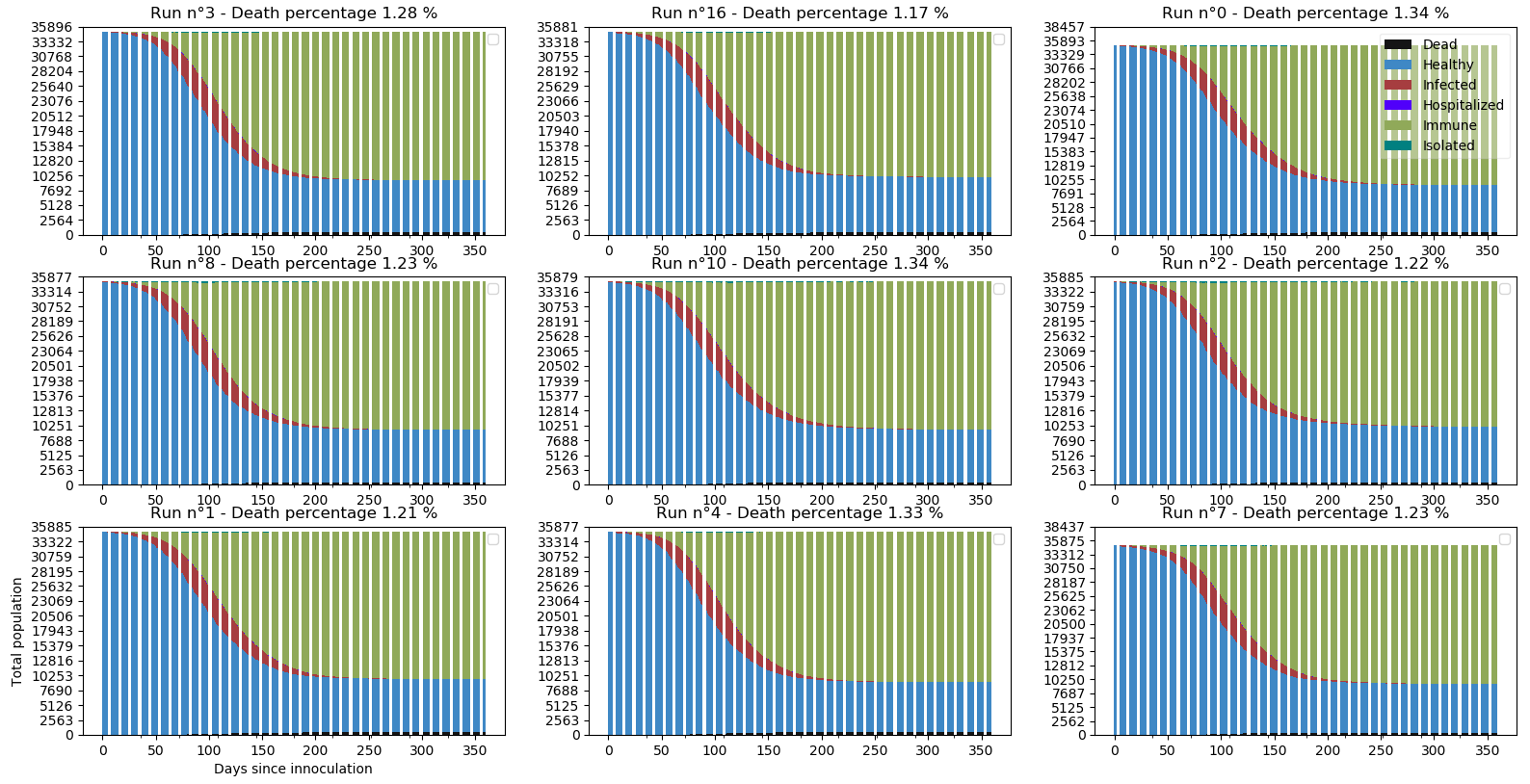
Ce scénario est similaire au scénario 0 où nous sommes allés chercher une immunité collective extrêmement lentement (900 jours) car le télé-travail avait été maintenu. Sauf qu’ici, l’immunité collective d’à peu près 60% d’infectés est plus rapidement atteinte (250 jours), et bien entendu en éreintant le système de santé (au maximum 10 fois la capacité marocaine, à priori aucun pays développé ne la possède).

Est-il possible de conclure que ne pas confiner tout en maintenant des probabilités de contagion très faible marche ? Probablement si on pense que tous les pays vont devoir chercher une immunité globale un jour ou l’autre, plutôt que d’éradiquer l’épidémie. J’imagine que les 1.26% de décès de population sont un prix à payer en attendant un vaccin.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 3 --extra 0  --draw exa pop summ lock hos new R0

Mais je reste sceptique, aucune population ne peut être civilisée au point de prendre des précautions extrêmes pendant 1 an. Testons une variante quelque peu insidieuse :
Chaque semaine, toutes les probabilités de contagion sont augmentées de 3% de manière à aboutir à une augmentation d’à peu près 500% au bout d’un an.

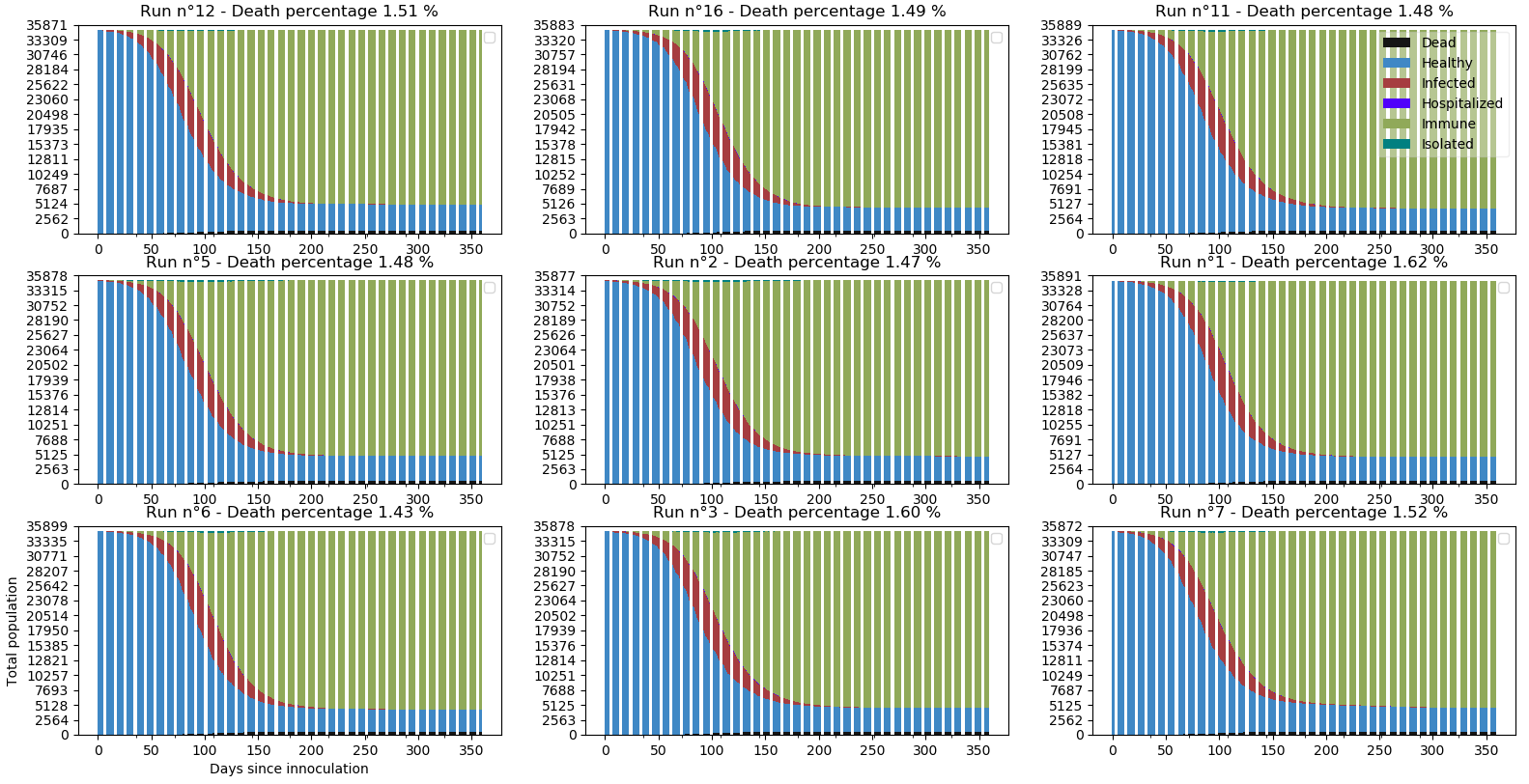
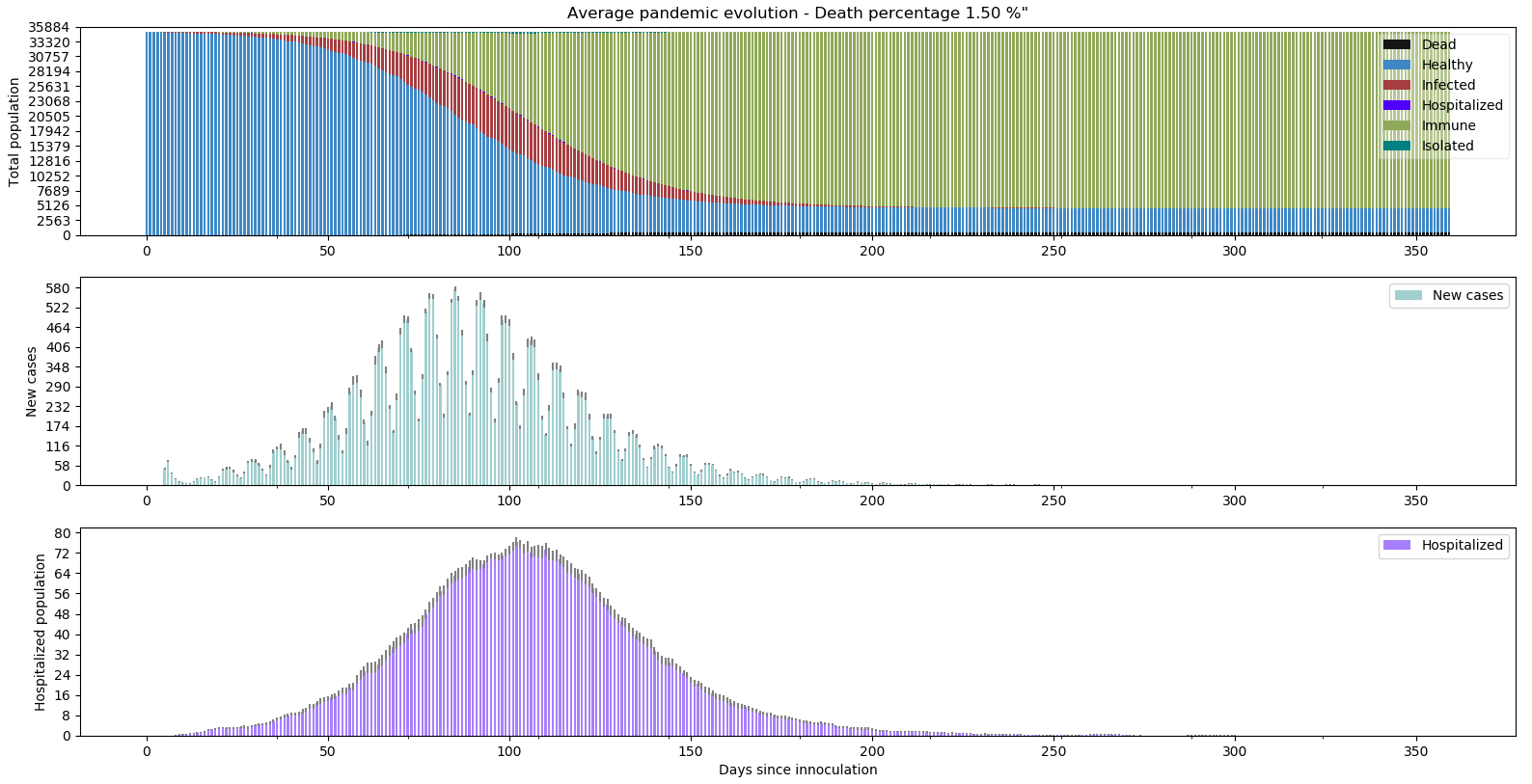
Sans surprise, il faut moins de 200 jours pour atteindre l’immunité collective (contre 250 précédemment). Au prix de quasiment 80% d’augmentation de la surcharge hospitalière et 0.3 points de mortalité en plus. En ayant gardé l’impact de la surcharge sur les taux de mortalités, nous aurions vu encore plus de morts. Je laisserais les spécialistes de l’éthique discuter la moralité de tels scénarios.

python -m scenario.run --nrun 20  --nday 360 --nind 3500 --scenario 3 --extra 0.03  --draw exa pop summ lock hos new R0 lock

Revenir à l’index

Takeaway scénario 3

L’immunité collective est-elle une réponse viable à une pandémie plutôt contagieuse mais globalement peu meurtrière (sauf le respect aux personnes qui ont perdu un proche ou un ami) ? Est-elle une solution morale ? Ethique ? Peut-être est-elle la seule solution dans un contexte de pandémie mondialisée. Les prochains mois nous diront ce qu’il en est.

Scénario 4 : Le risque latent des incivilités individuelles (dit scénario du rogue citizen)

Le scénario 0 avec confinement strict a été adopté par les autorités. Ce sera difficile pour la population mais il faut tuer la pandémie au plus vite. Par contre, il existe un peu partout un certain nombre de citoyens infectés qui ne respectent pas les consignes de protection sanitaire. Ce sont les fameux super spreaders ^{[19] [20]}.

Considérons donc les paramètres de ce scénario avec l’ajustement suivant :

• Chaque jour, on prend plusieurs personnes contagieuses au hasard et on multiplie par 10 leur indice de comportement individuel ce qui le ramène entre 500% et 1500% (ce qui signifie que les probabilités de contagion avec ces individus sont multipliées par 5 à 30…). Un tel individu ne respectant donc pas les règles de précaution élémentaires, il va sans dire que le champion se rend sur son lieu de travail…

Le confinement strict peut-il vaincre quelques incivilités isolées ?

Mais d’abord, reprenons une illustration du scénario 0. Voici comment meurt la pandémie en confinement strict (la durée des simulation est réduite à 180 jours) :

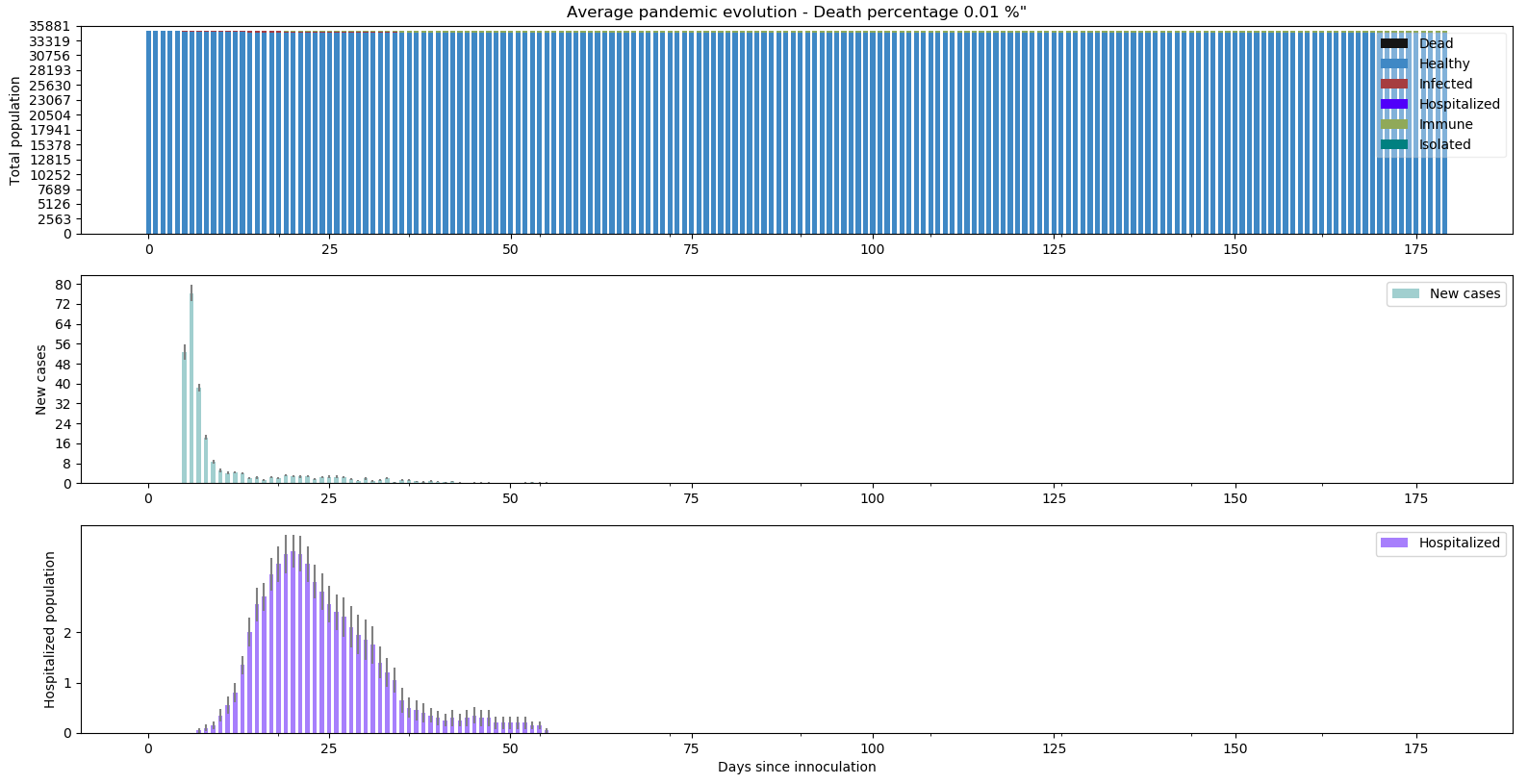
Pas de surprise, nous connaissions ces résultats.

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario 4 --extra 0 10  --draw pop summ

Testons à présent avec une seule et unique personne contagieuse au comportement irresponsable par jour :

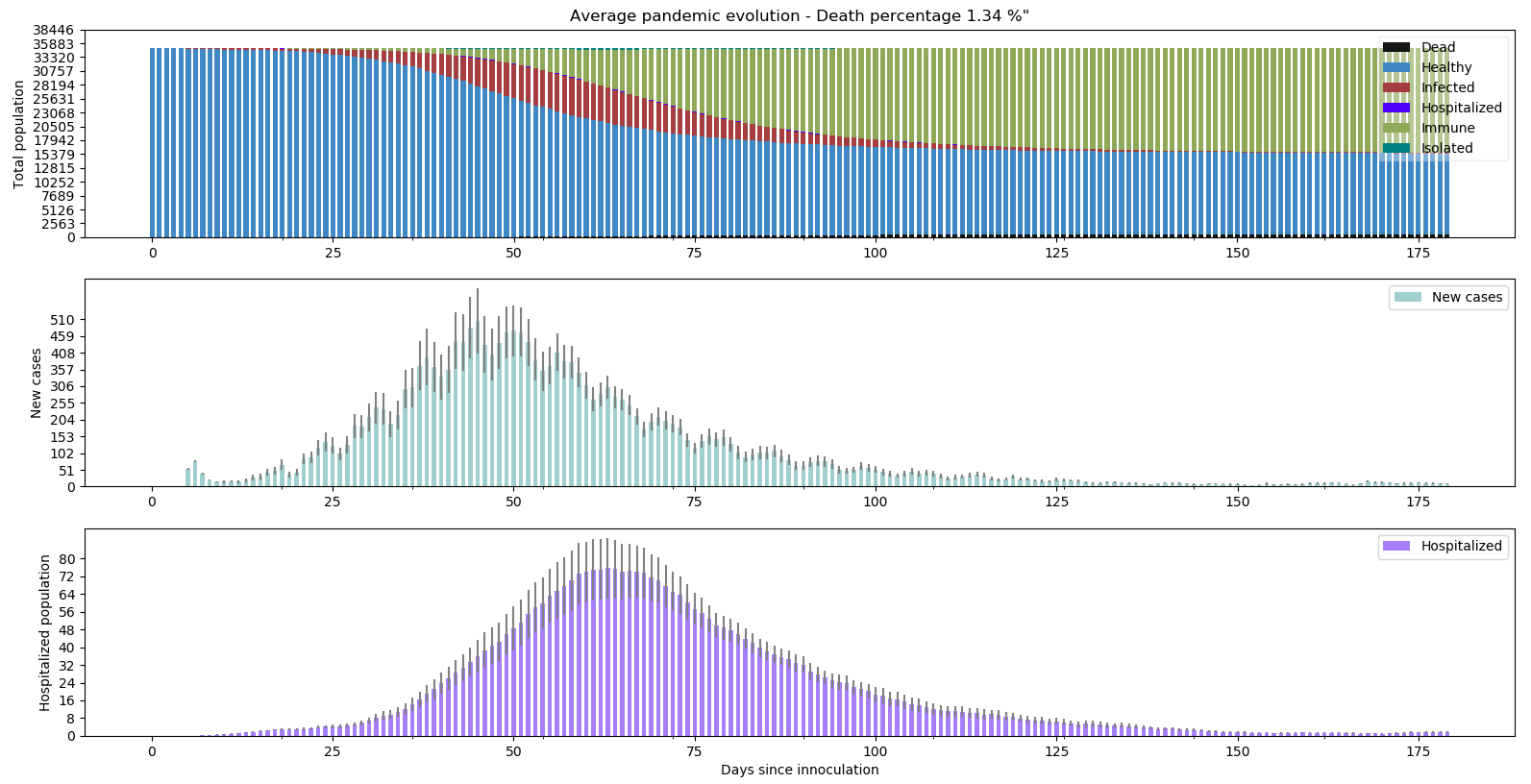
Une seule personne par jour a suffit pour alimenter la pandémie et ruiner en moyenne l’effort de 35000 personnes !

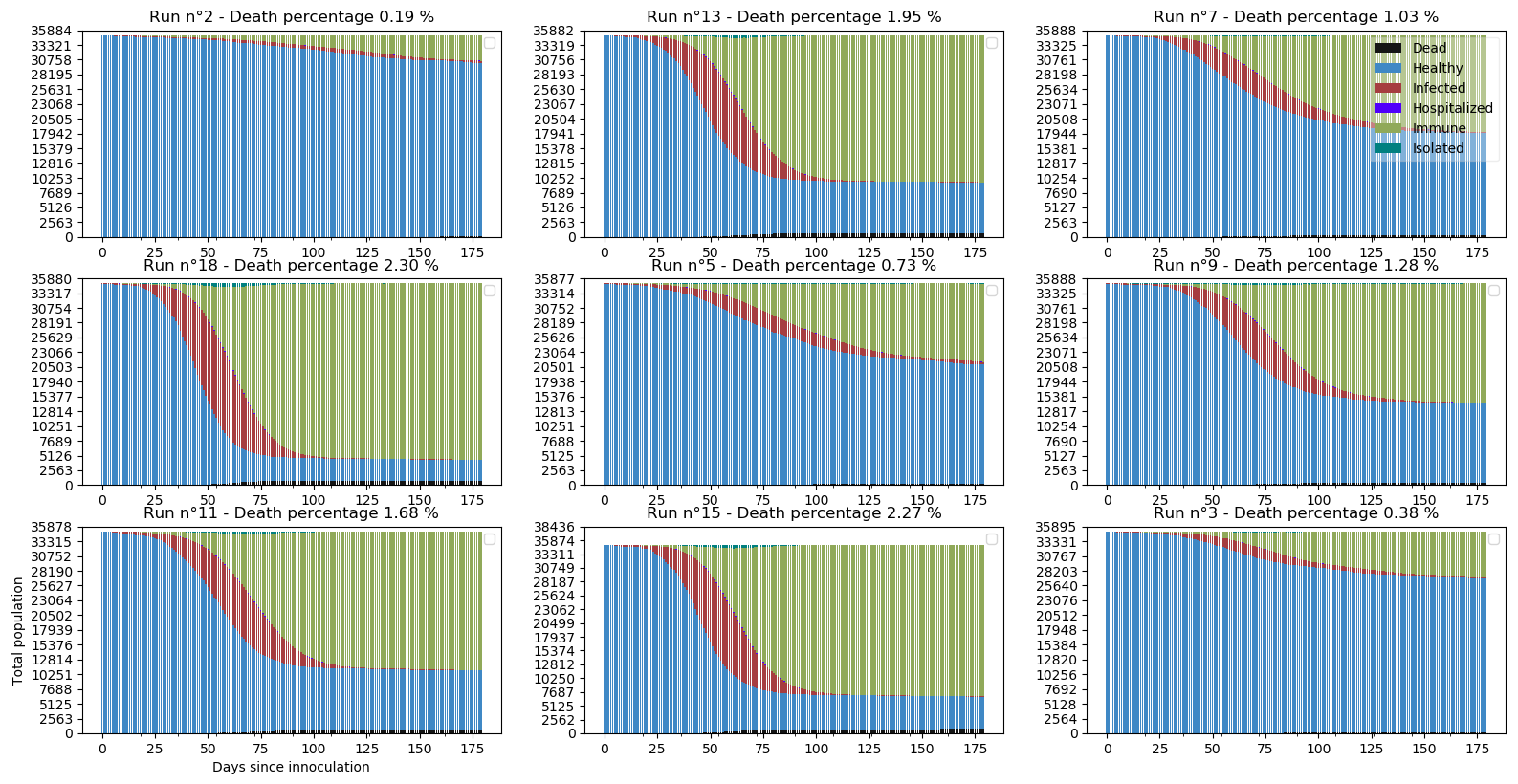
C’est aussi globalement une question de chance. Les simulations n°2 et n°3 s’en sortent honnêtement avec des pourcentage de décès de 0.19% et 0.38%. Mais dans la simulation n°18, on retrouve quasiment le scénario X avec des proportions de décès de plus de 2%. Il est fascinant de voir la sensibilité de notre modèle de confinement au comportement de quelques individus isolés

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario 4 --extra 1 10  --draw exa pop summ lock hos new R0

Takeaway scénario 4

Il faut tester le plus massivement possible. Dépister et isoler car le type d’individu que nous avons modélisé existe dans notre société sans que nous lui prêtions toute mauvaise intention. C’est le vendeur de figue de barbarie (moul lkarrossa) dans la rue, c’est le responsable de rayon de supermarché quelque peu négligent, c’est le conducteur de taxi qui ne porte pas de masque. Nos sociétés fragiles sont sensibles à ce genre d’aléas. Si nous ne permettons pas au plus grand nombre ou à minima à ces individus très exposés d’être dépistés régulièrement, nous nous exposons à ruiner l’effort de confinement et à revenir naturellement au scénario 3 d’immunité collective en ayant gaspillé de précieux mois de confinement strict.

Revenir à l’index

Scénario 5 : Le foyer persistent (dit scénario du quartier rebelle)

Si au lieu d’avoir des individus irresponsables, nous avions un quartier entier mais avec un indice de comportement seulement légèrement plus important que les autres quartiers. A travers ce scénario, nous cherchons à modéliser des quartiers pour lesquels la confinement est structurellement et socialement difficile ^[21]. Le confinement strict peut-il cette fois-ci battre un quartier entier ?

Nous avions évoqué dans nos hypothèses le système de grille et de quartiers. Il y en a par défaut 400.

Prenons 4 quartiers au hasard (donc à peu près 1% des foyers) et multiplions leur indice de comportement par 10 comme dans le scénario précédent :

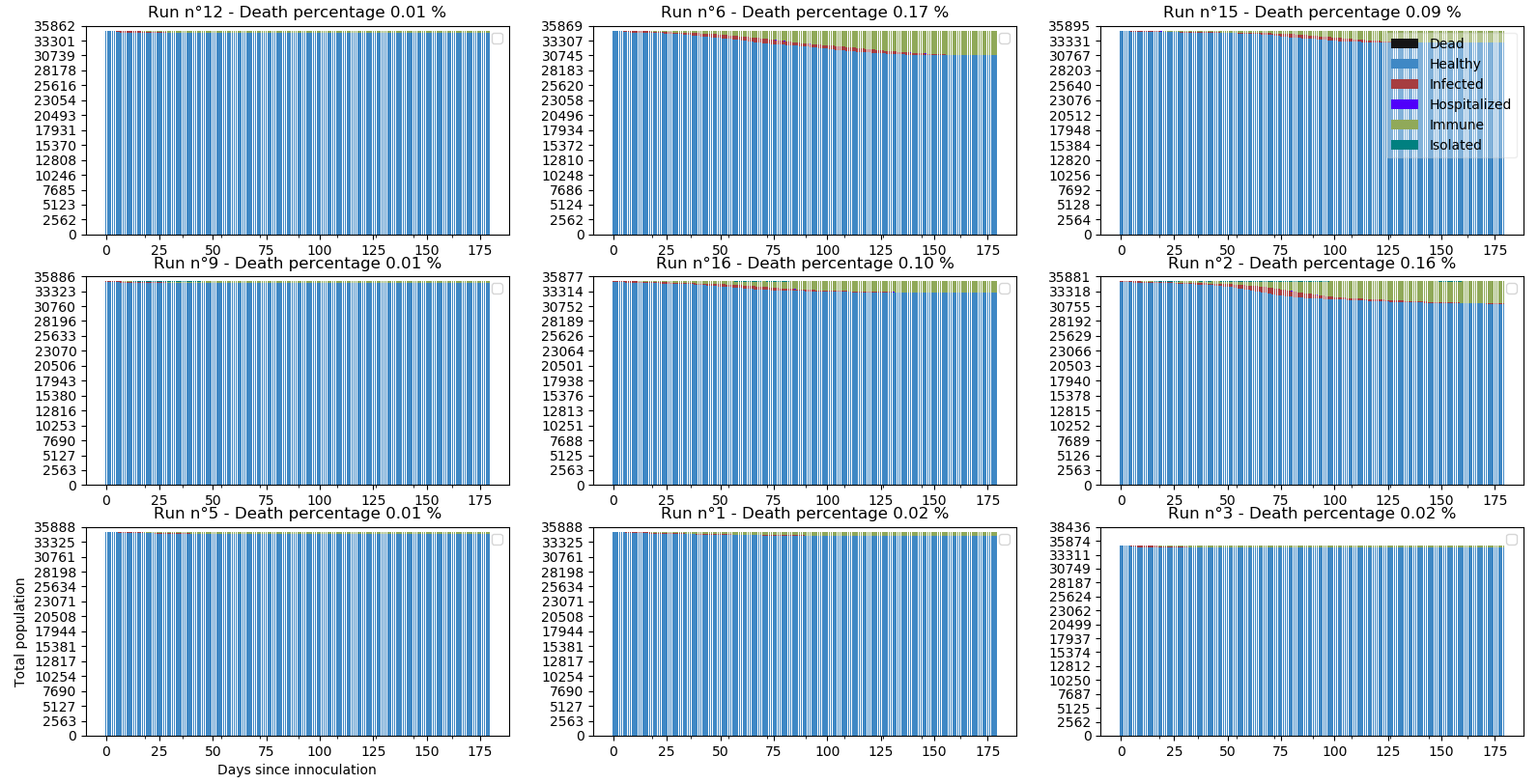
On s’attendait à une explosion de cas mais non. Le confinement est plus fort qu’une minorité incivile sauf dans les simulations n°2 et n°6 pour lesquelles la pandémie se maintient légèrement. Le scénario précédent ciblait précisément les personnes contagieuses et ajoutait une chaque jour alors qu’ici nous avons pris 1% de la population (315 personnes en moyenne soit quasiment le même nombre que les 360 ou 1 par jour du scénario 6).

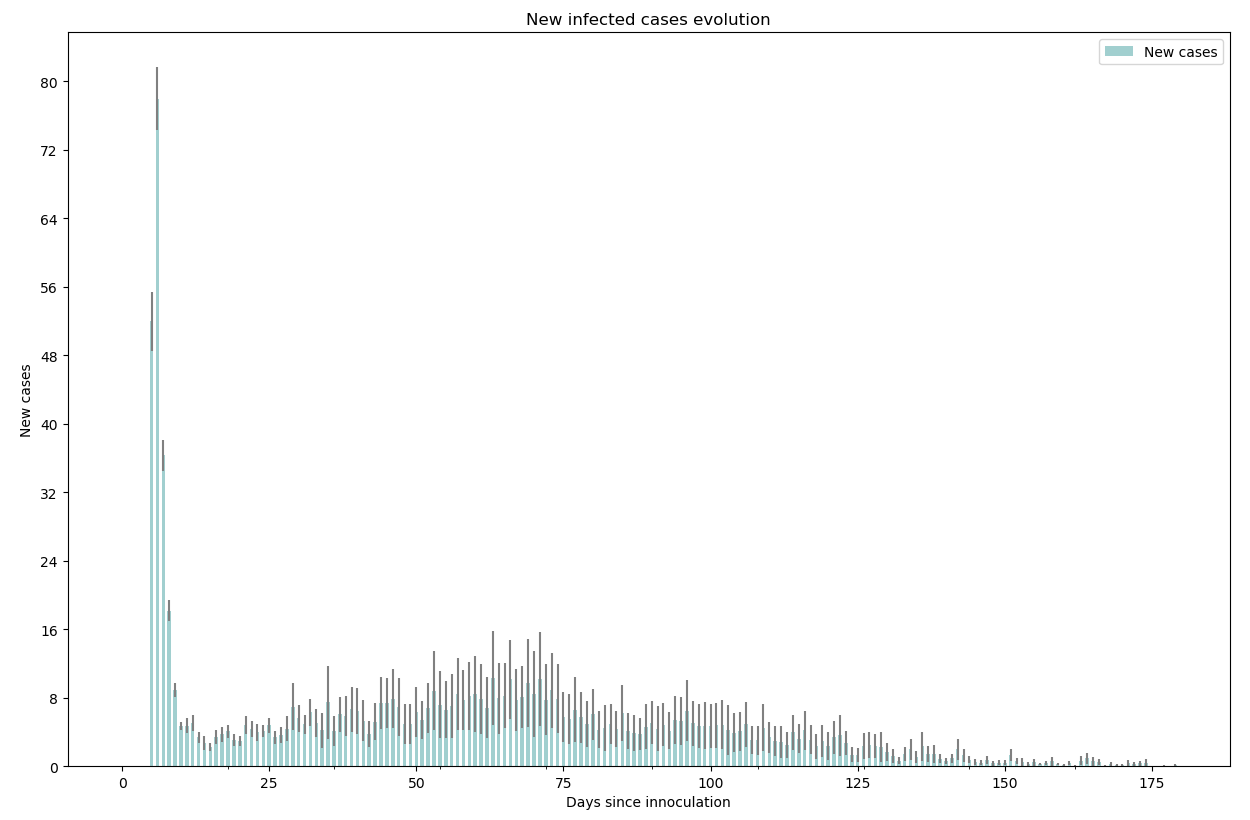
Le nombre de nouveaux cas reste tout de même persistant sur plusieurs mois alors qu’on a vu précédemment que le confinement strict tuait la pandémie au bout d’une cinquantaine de jours. L’impact n’est donc pas négligeable.

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario 5 --extra 4 10  --draw exa pop summ lock hos new R0

Takeaway scénario 5

Là encore, tout nous pousse à croire que c’est la détection et isolation précoce des infectés qui prime sur le comportement général de la société. La plupart des gens ne sont pas infectés. Leur comportement n’impacte que très peu le sort de la pandémie. Par contre, quelques individus lorsqu’ils sont contagieux peuvent avoir un pouvoir énorme sur la propagation du virus.

Revenir à l’index

Scénario 6 : Les cas importés (dit scénario du voyageur)

Restons toujours dans la situation de confinement strict mais imposons qu’il y ait un certain nombre de personnes infectées qui arrivent chaque jour dans notre pays. Ce sont des touristes, des MRE, des hommes d’affaire …

Avec par exemple une personne infectée par jour qui s’ajoute à la population, le confinement strict est-il suffisant pour contrôler la pandémie (qui ne peut du coup pas s’arrêter par construction) et l’empêcher de s’emballer ?

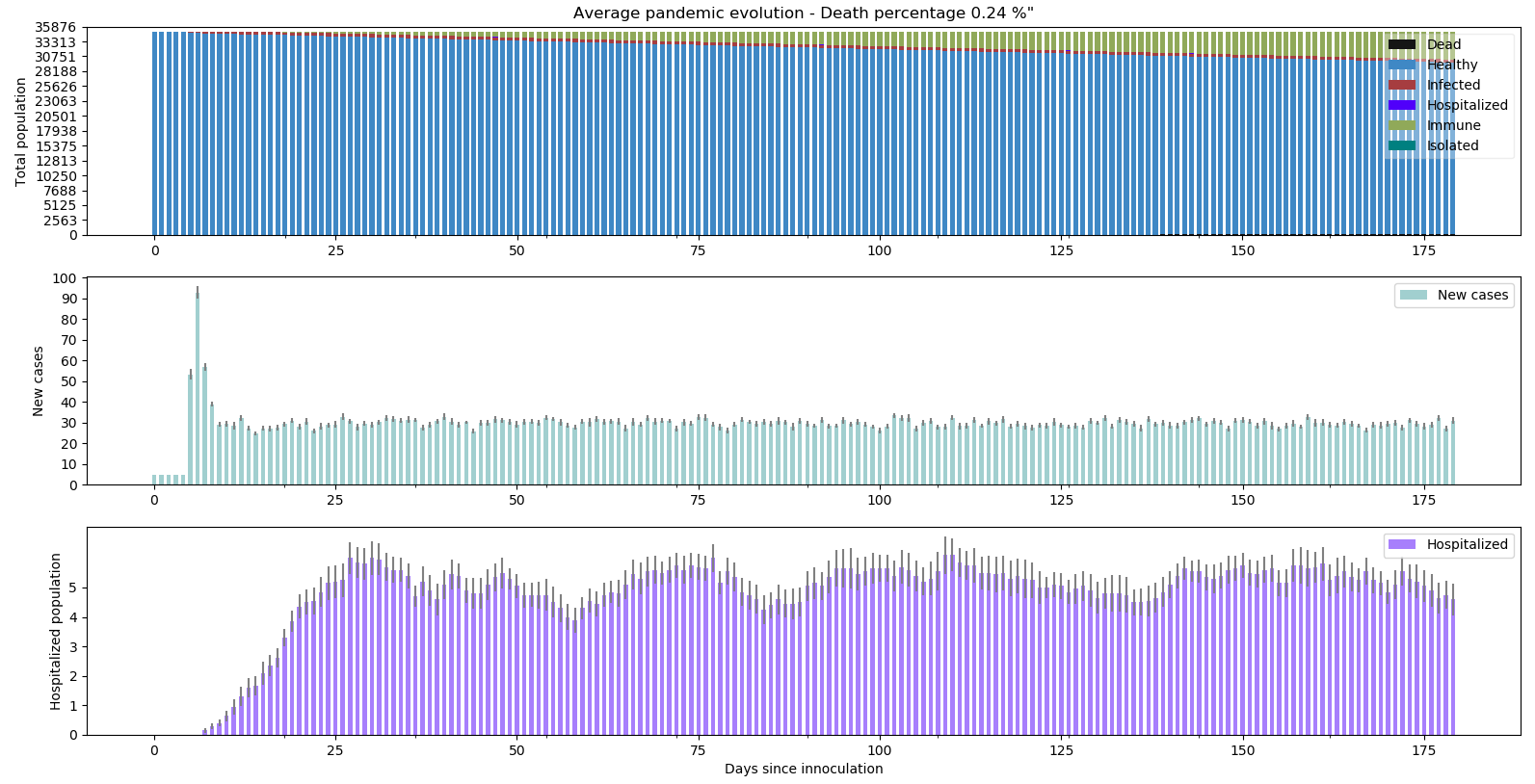
Pas de problème tant que les cas importés sont en nombre plutôt faible. La pandémie est parfaitement contrôlée même si ces cas provoquent une saturation des hôpitaux.

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario 6 --p-store 0.001 --extra 5  --draw exa pop summ lock hos new R0

Si nous continuons ce raisonnement avec cette fois-ci 50 cas importés par jour :

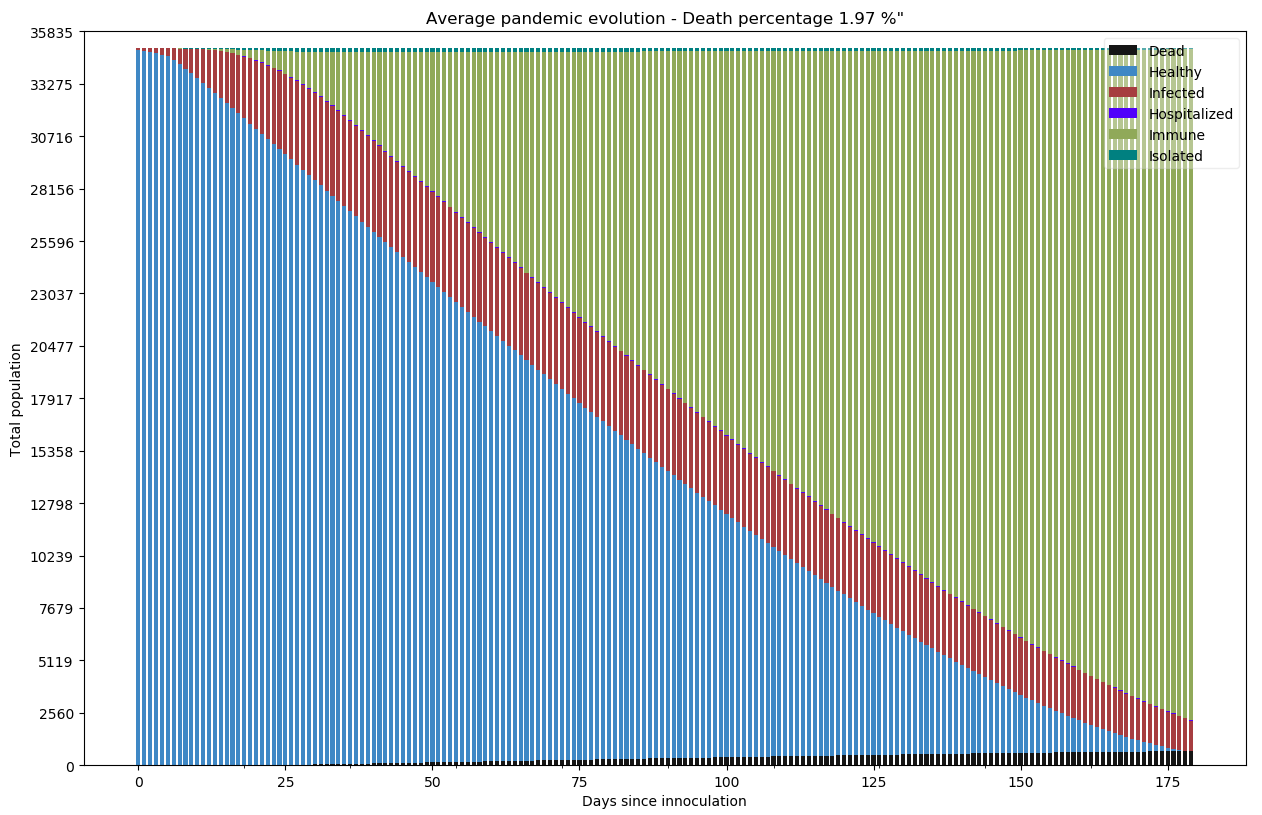
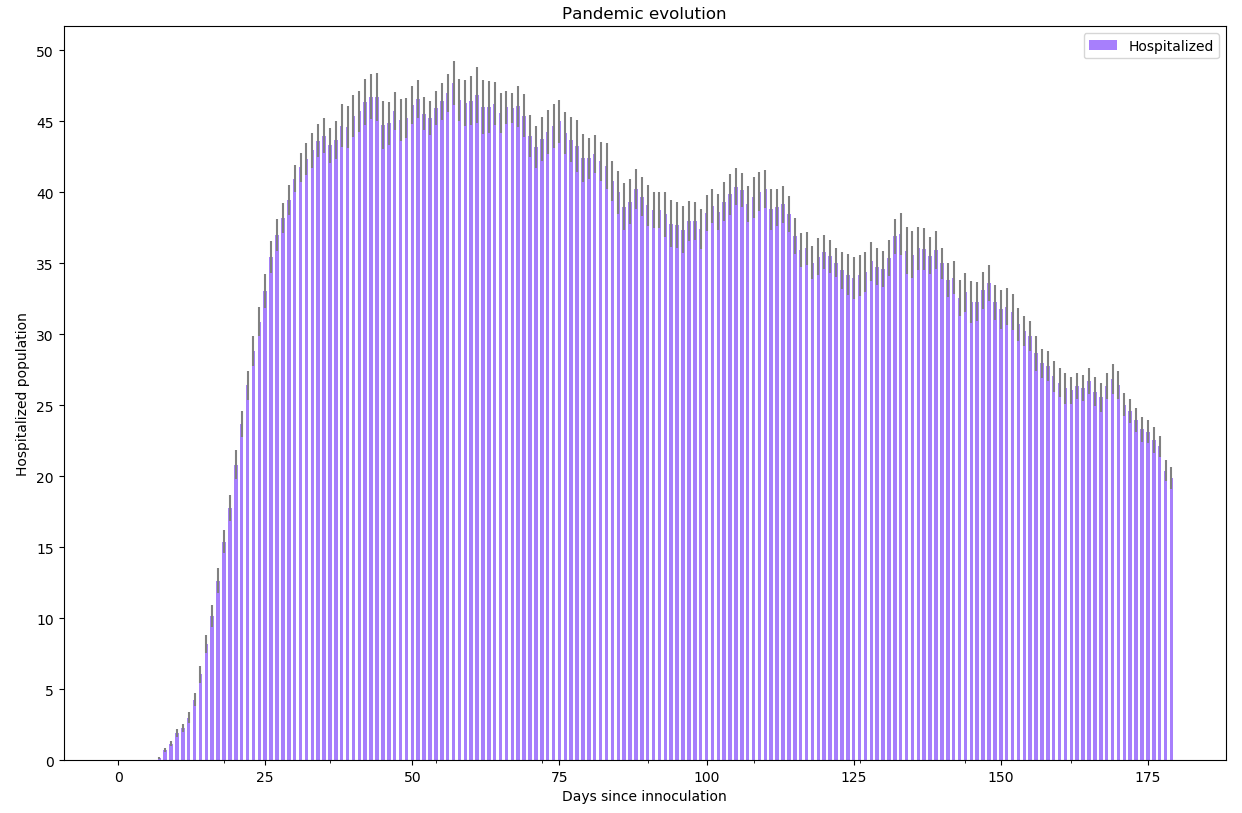
L’augmentation semble plus linéaire qu’exponentielle même si le niveau de saturation des hôpitaux est évidemment très élevé.

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario 6 --p-store 0.001 --extra 50  --draw exa pop summ lock hos new R0

L’évolution est-elle exponentielle avec respectivement pour les deux graphes suivants 5 puis 50 cas importés par jour en situation de confinement normal plutôt que strict ?

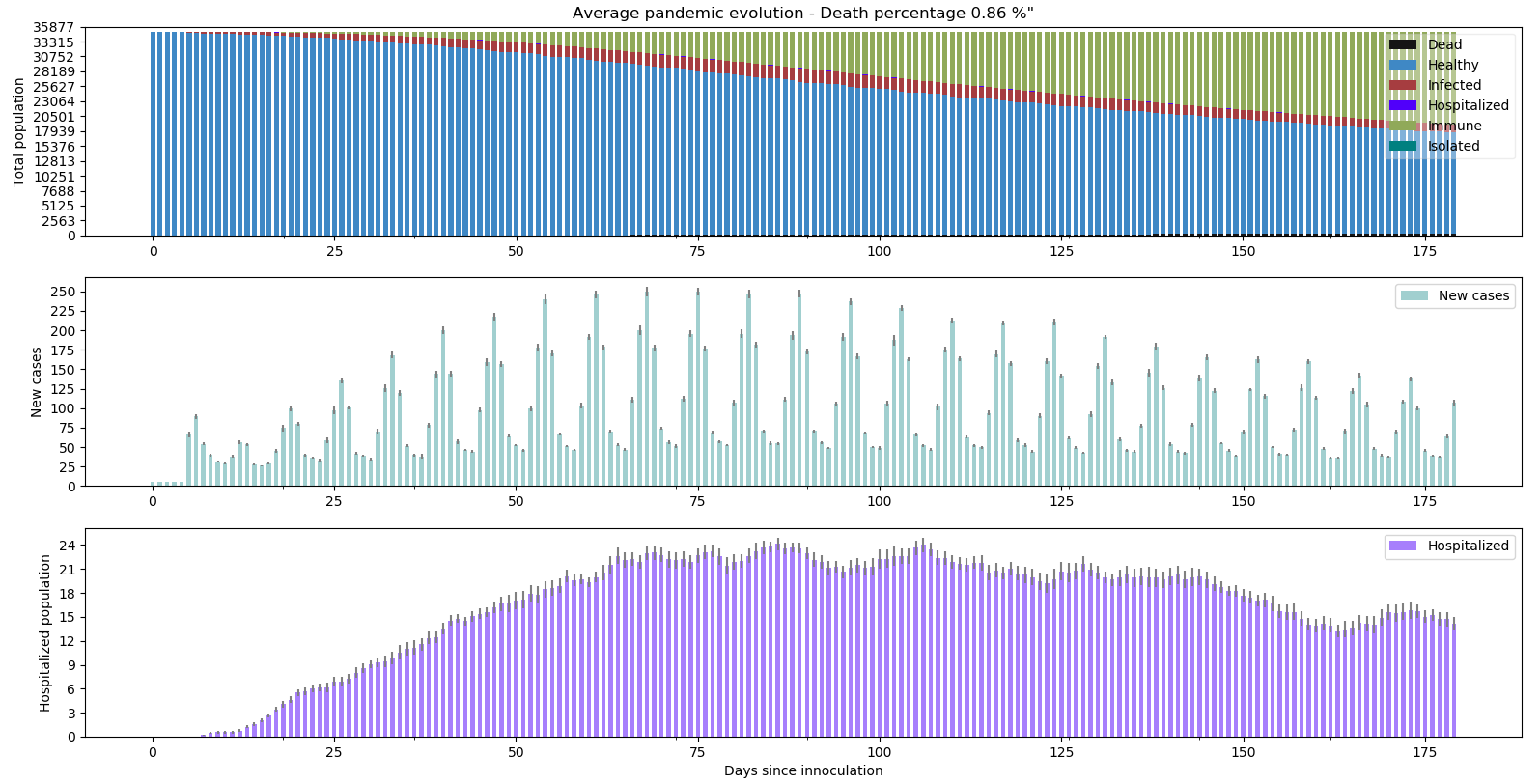
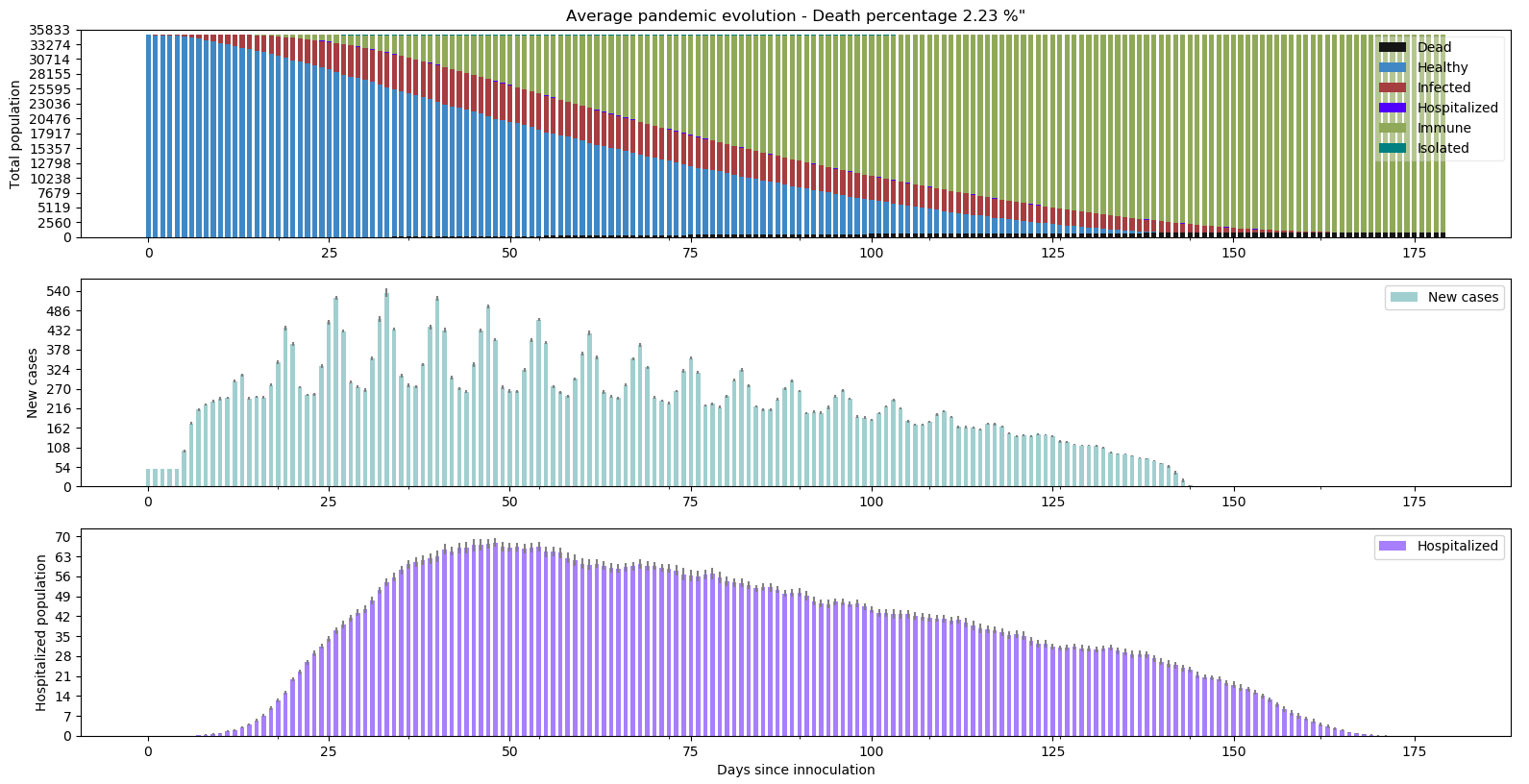
Toujours pas. Ce paramètre ne semble pas jouer sur le type de comportement de la pandémie.

python -m scenario.run --nrun 20  --nday 180 --nind 35000 --scenario 6 --p-store 0.02 --extra 5  --draw exa pop summ lock hos new R0

Takeaway scénario 6

La pandémie en confinement résiste bien aux infections exogènes. Faut-il ouvrir les frontières pour autant ? Je ne m’avancerais pas là-dessus mais je ne suis pas étonné qu’un pays comme la Chine qui ne cherche pas à enrayer l’épidémie mais à la circonscrire ait relancé son trafic aérien ^[22].

Revenir à l’index

Scénario 7 : L’immunité temporaire (dit scénario de la grippe saisonnière)

Nous terminerons cette dense étude par l’immunité temporaire. Une fameuse étude sud-coréenne expliquait que certains patients testés négatif après avoir été infectés montraient une charge virale qui augmentait peu de temps après. ^{[1] [2]}. L’idée qu’il existe une possibilité de rechute face au Covid-19 paraît insoutenable car elle condamnera nos société à vivre dans un confinement permanent ou à sacrifier toutes les personnes exposées. En attendant un vaccin.

Confrontons quelques uns de nos scénarios les plus encourageants à l’immunité temporaire.

Scénario 0 - Confinement strict : On a vue que le confinement strict était très efficace pour éteindre une pandémie en 50 à 60 jours. Pour le tester, nous allons utiliser une immunité très court de 10 à 15 jours et chercher des cas où la fin de la pandémie est retardé :

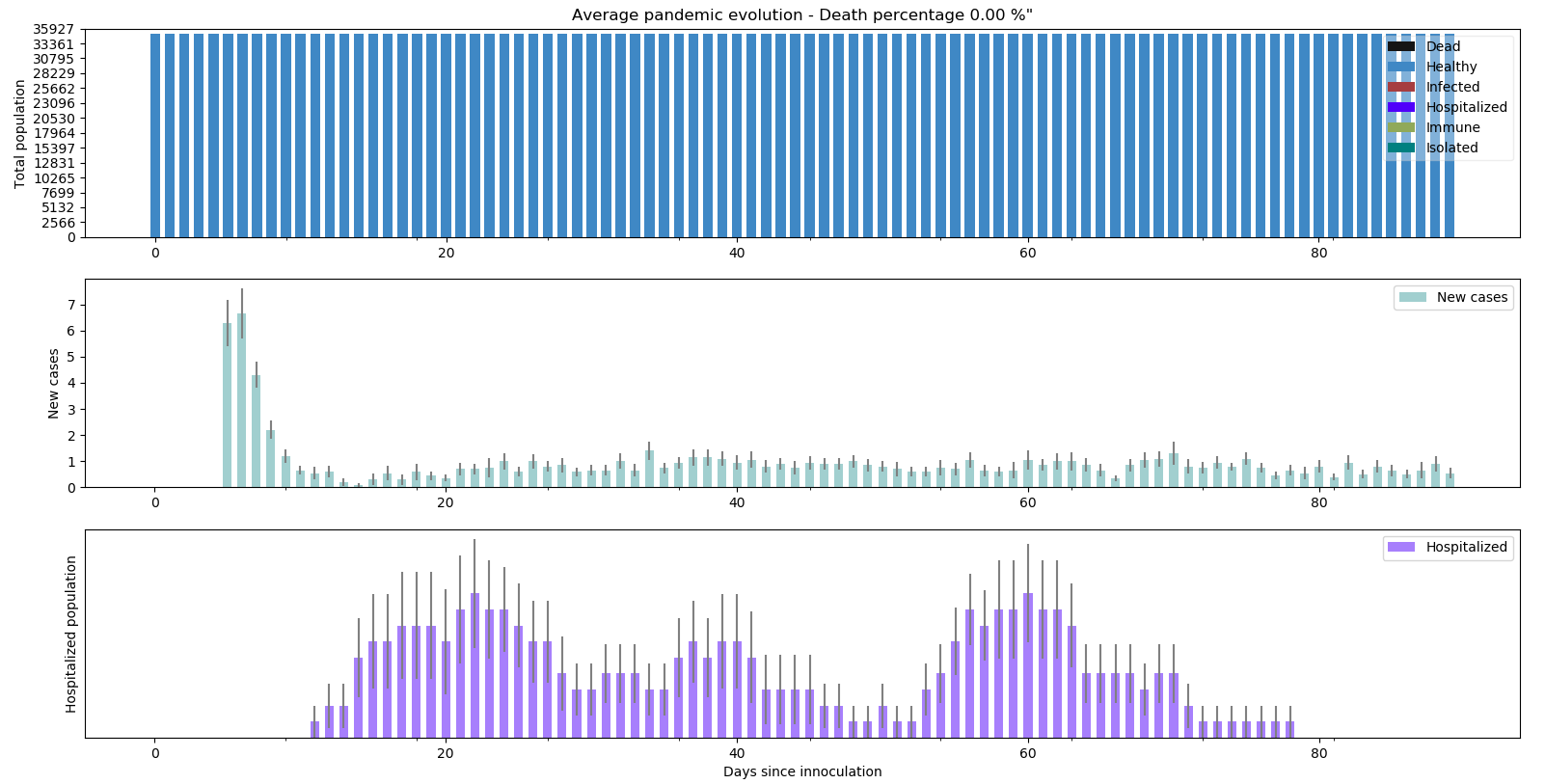
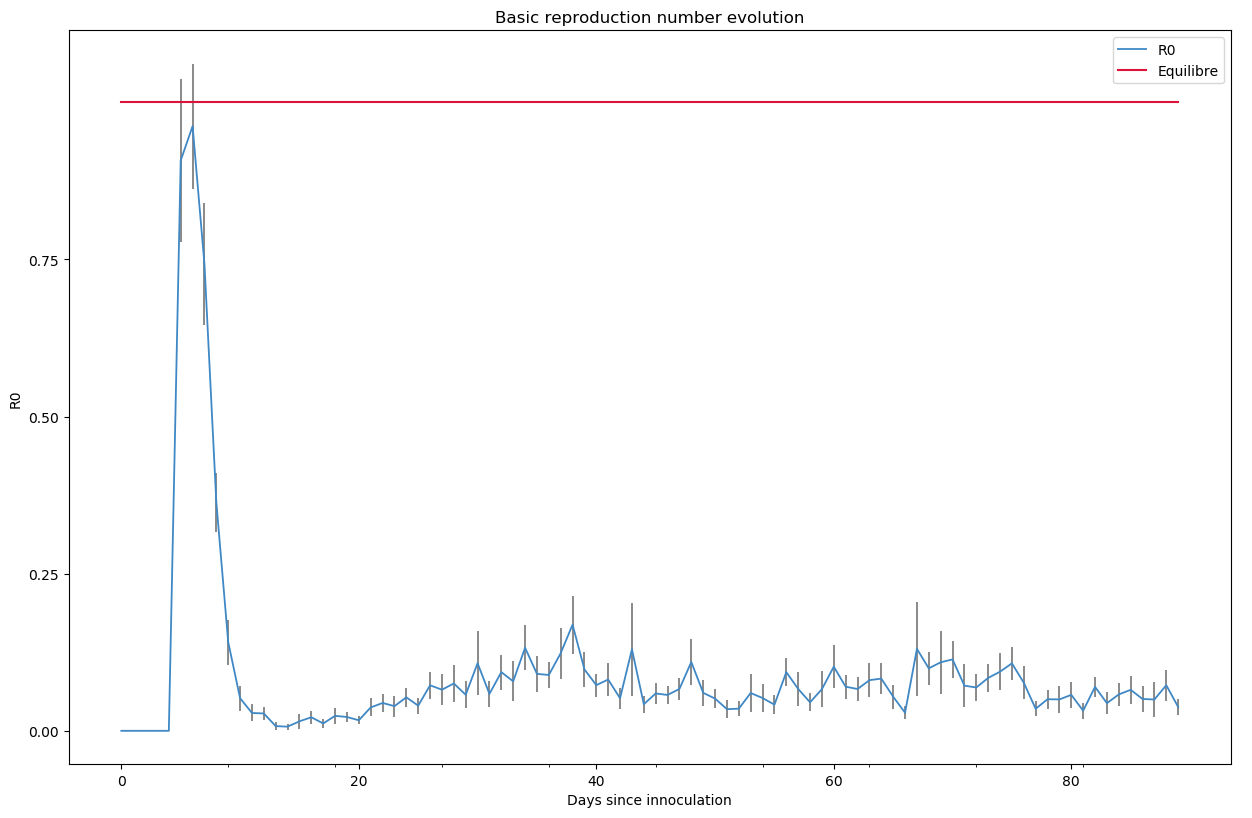
L’épidémie se comporte plutôt bien mais refuse de s’éteindre comme en témoigne le R0 qui oscille au-dessus de 0. Je pense que les infections deviennent cycliques dans les maisons et les lieux de travail en raison de la faible durée de l’immunité. Les hospitalisations semblent s’arrêter au 80ème jour mais globalement la situation est maîtrisée.

python -m scenario.run --nrun 20  --nday 90 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.001 --imm 10 15 --draw exa pop summ R0

Scénario 0 - Confinement normal : Le confinement normal permettait de maintenir l’épidémie dans des proportions gérables. Nous avions même observé une immunité collective au bout de 900 jours. Mais par définition, il ne peut plus y avoir d’immunité maintenant. Alors comment va réagir l’épidémie ?

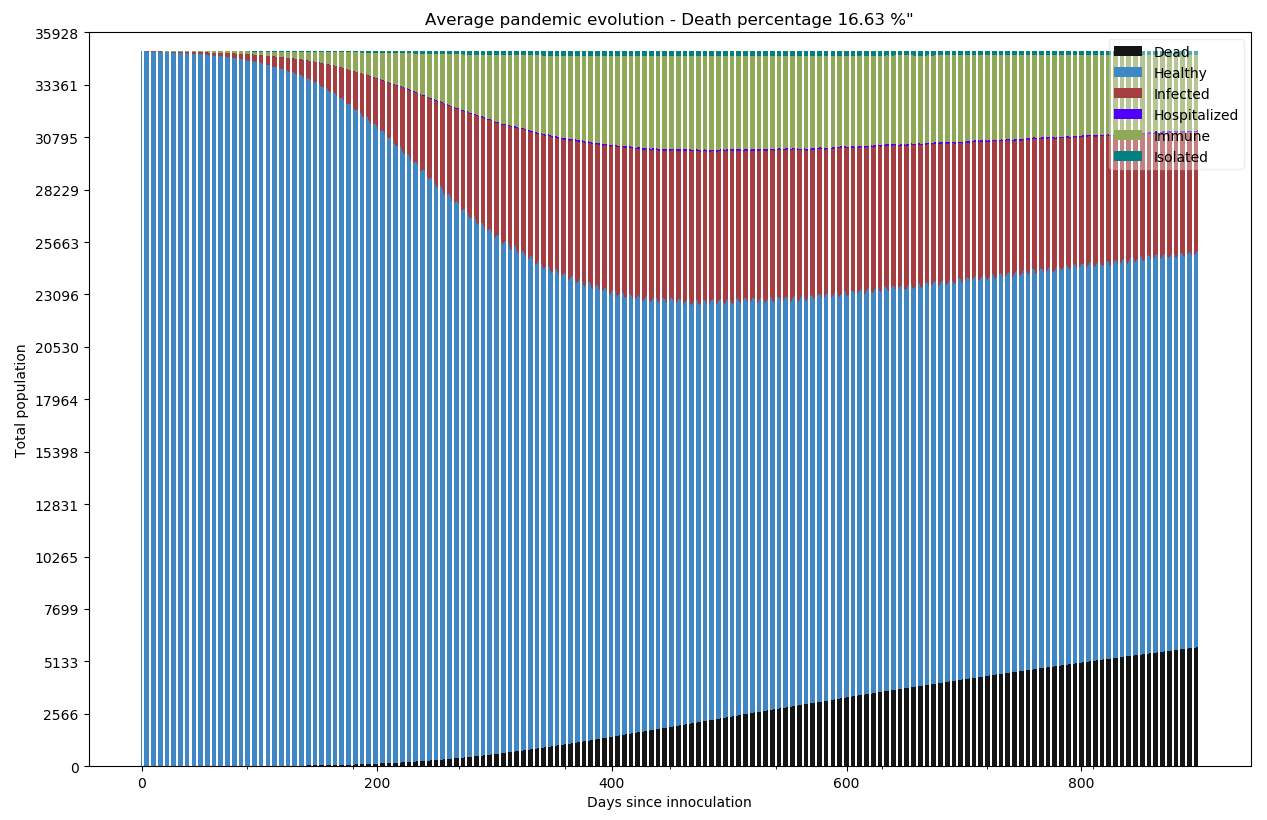
Très mal. Le réservoir de personnes immunisées ne parvient pas à augmenter suffisamment pour atteindre une immunité collective et étouffer la pandémie. Le résultat logique est l’augmentation énorme du nombre de personnes décédées à 16% en arrêtant la simulation à 900 jours. Cela s’apparente à un lancer de dé : Même si vous réchappez au virus une fois, 10 à 15 jours plus tard, vous redevenez candidats à une infection et donc soumis aux tables de mortalité. Et ainsi de suite jusqu’au décès de suffisamment de personne pour atteindre une “immunité” collective arithmétique provoquée par l’amputation d’une grosse partie de la population. Le scénario n’est pas joyeux. Allons voir ailleurs.

# Attention, cette simulation prend près de 25 minutes
python -m scenario.run --nrun 20  --nday 900 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.02 --imm 10 15 --draw exa pop summ R0

En passant la durée de l’immunité à des valeurs plus réalistes : 60 à 90 jours, voici l’évolution du confinement normal sur 900 jours.

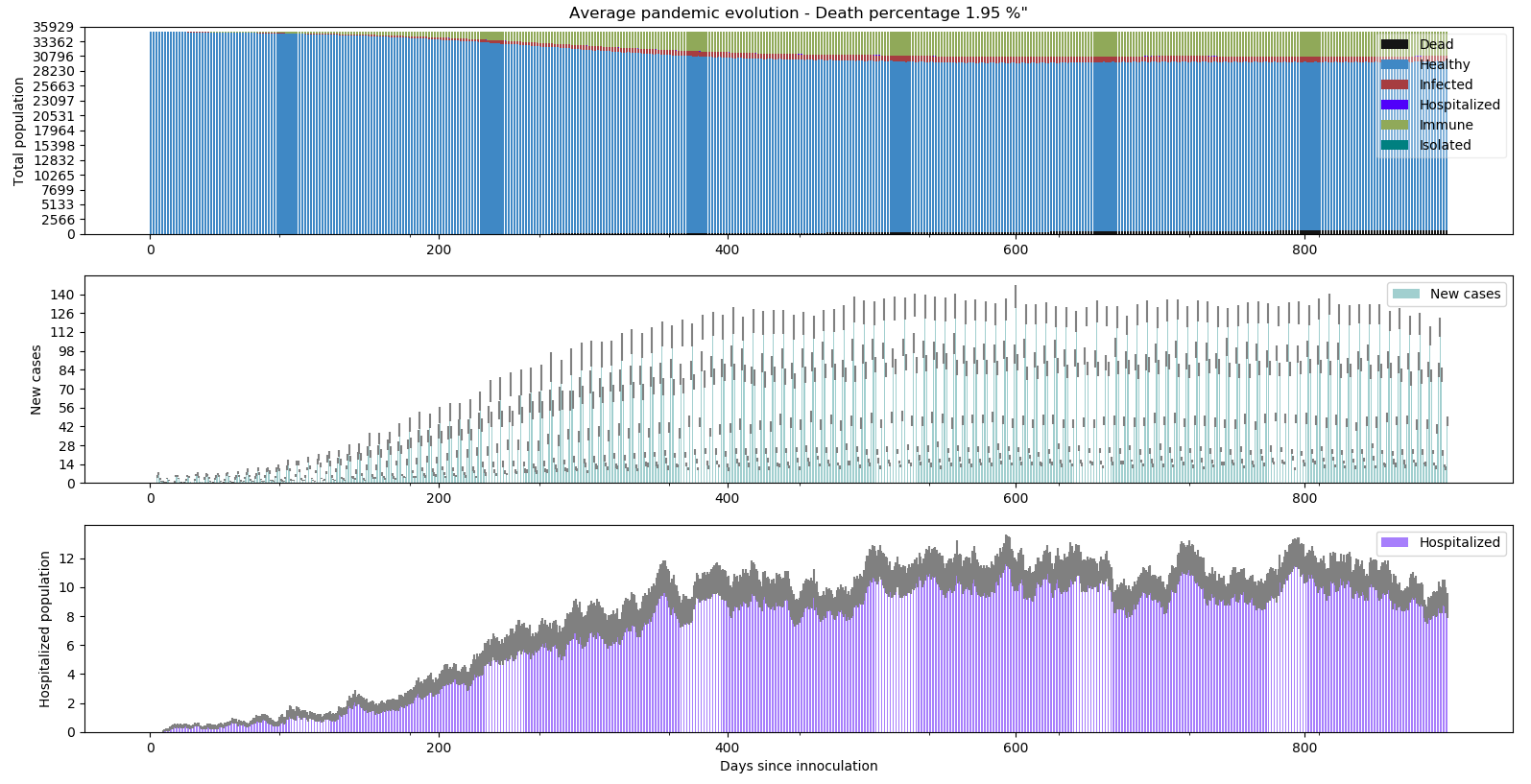
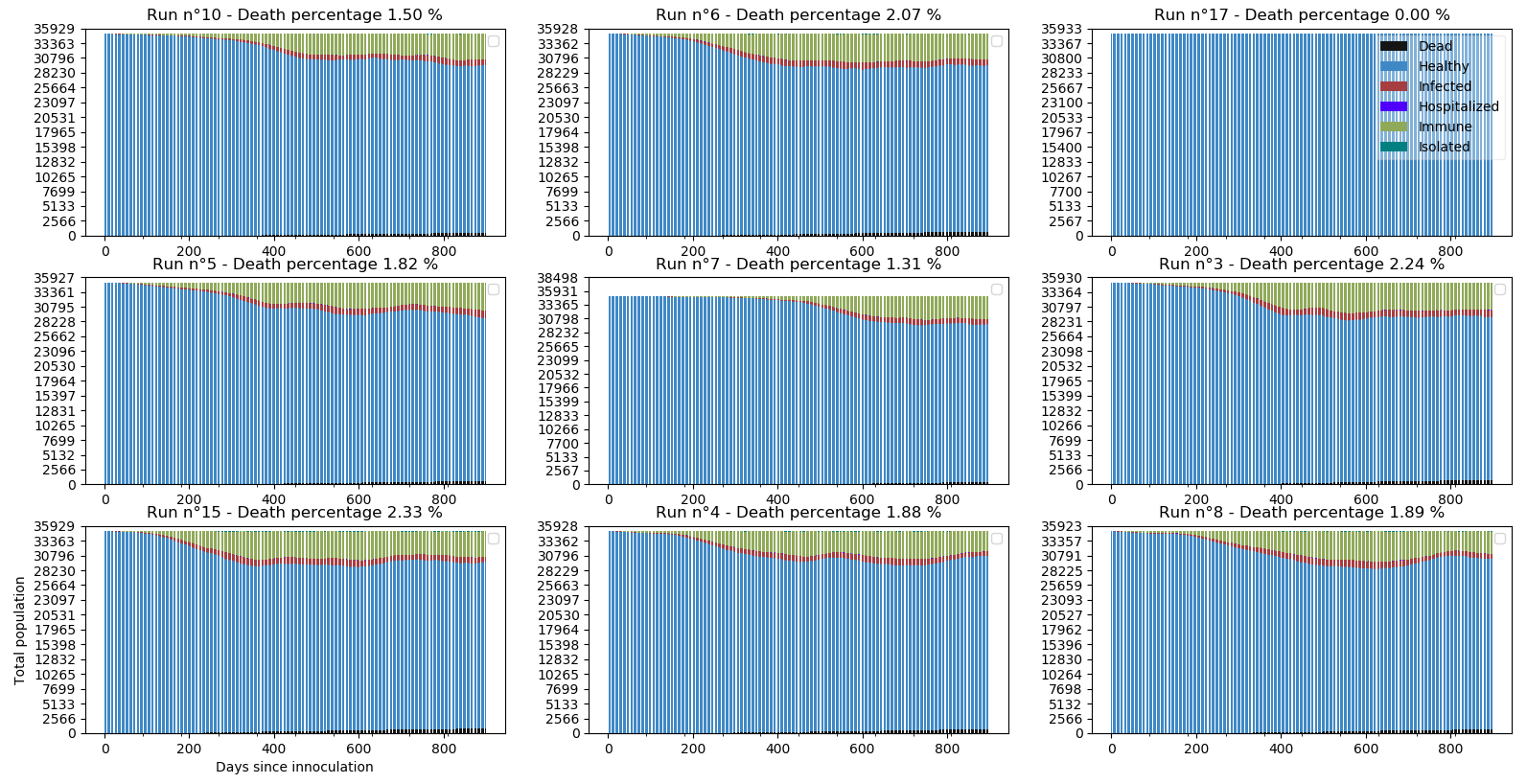
Là aussi, aucune immunité collective n’est atteinte au bout des 900 jours. Prolonger l’immunité ralentit l’augmentation du nombre de décès mais ne semble pas enrayer l’épidémie. Notons quand même que sur le graphe des simulations individuelles, la simulation n°17 a vu l’épidémie s’éteindre comme cela peut arriver lorsque la chance est de notre côté.

# Attention, cette simulation prend près de 25 minutes
python -m scenario.run --nrun 20  --nday 900 --nind 35000 --scenario 0 --p-house 0.5 --p-work 0.01 --p-transport 0.01 --p-store 0.02 --imm 60 90 --draw exa pop summ R0

Scénario 2 - Le yo-yo après 14 jours : Gardons l’immunité de 60 à 90 jours et analysons son effet sur le scénario où on déconfinait et reconfinait en fonction de l’évolution de la situation :

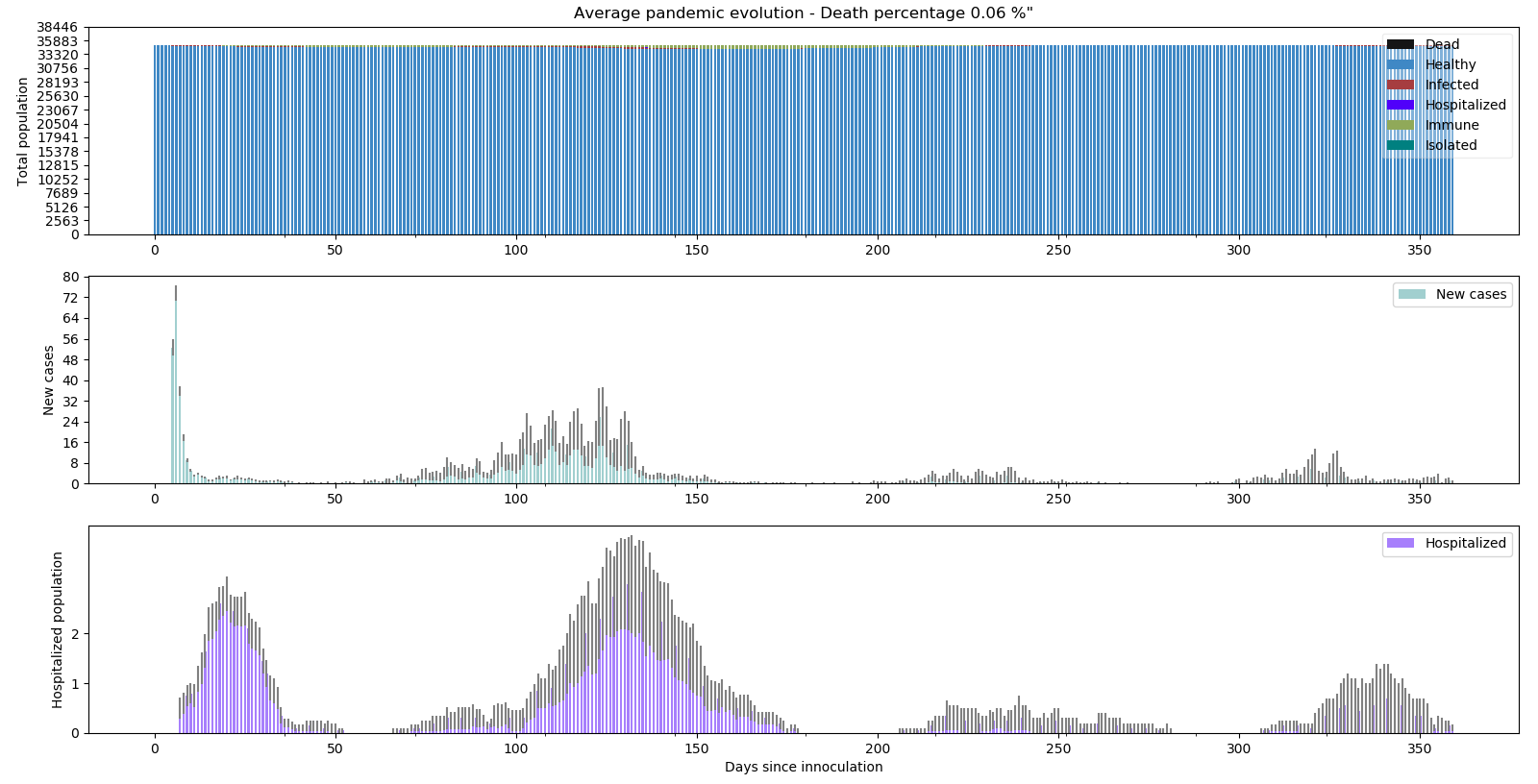
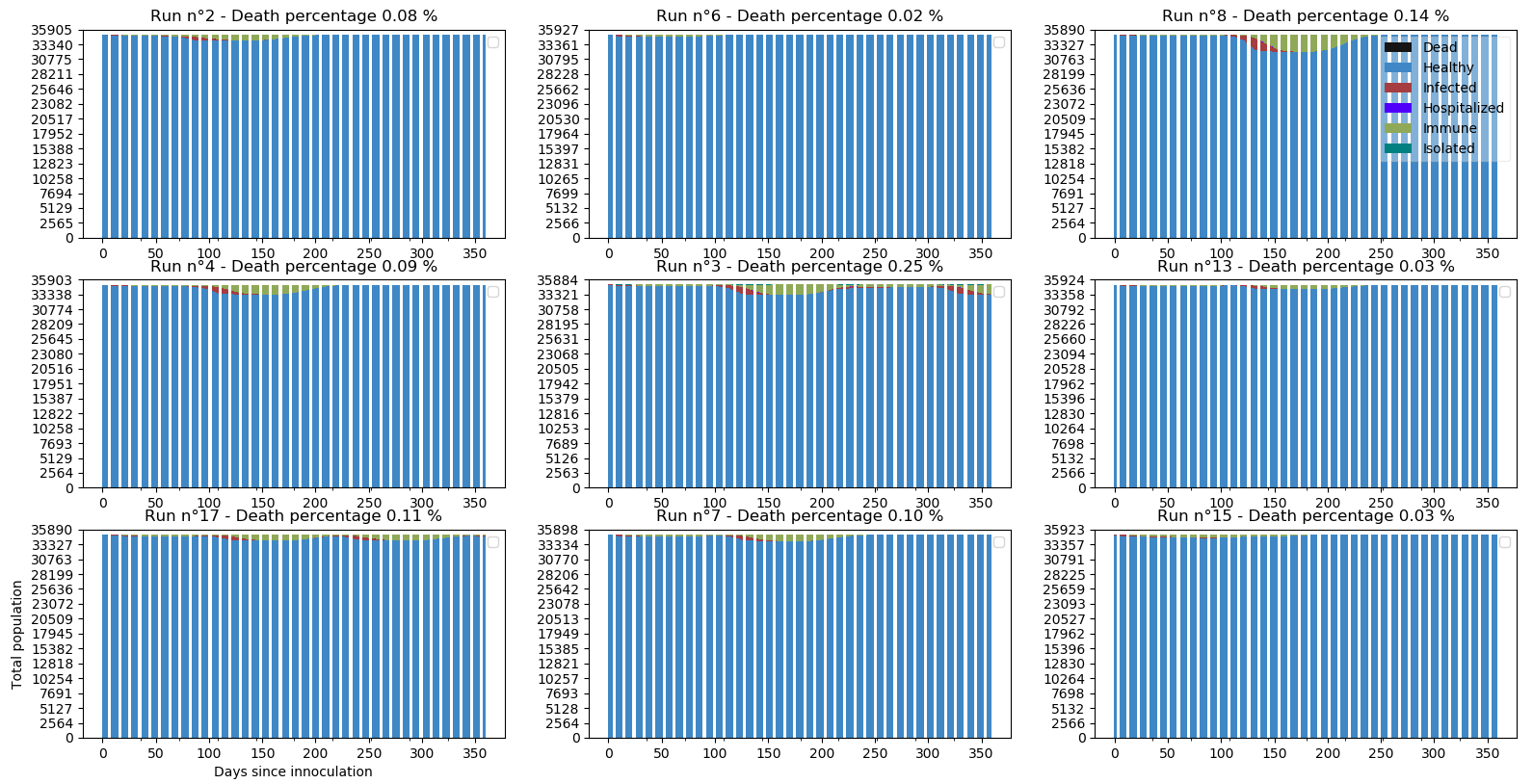
Le scénario du yo-yo s’est correctement adapté à la situation malgré des explosions de nouveaux cas comme par exemple sur la simulation n°8 rapidement rattrapée par le resserrement.

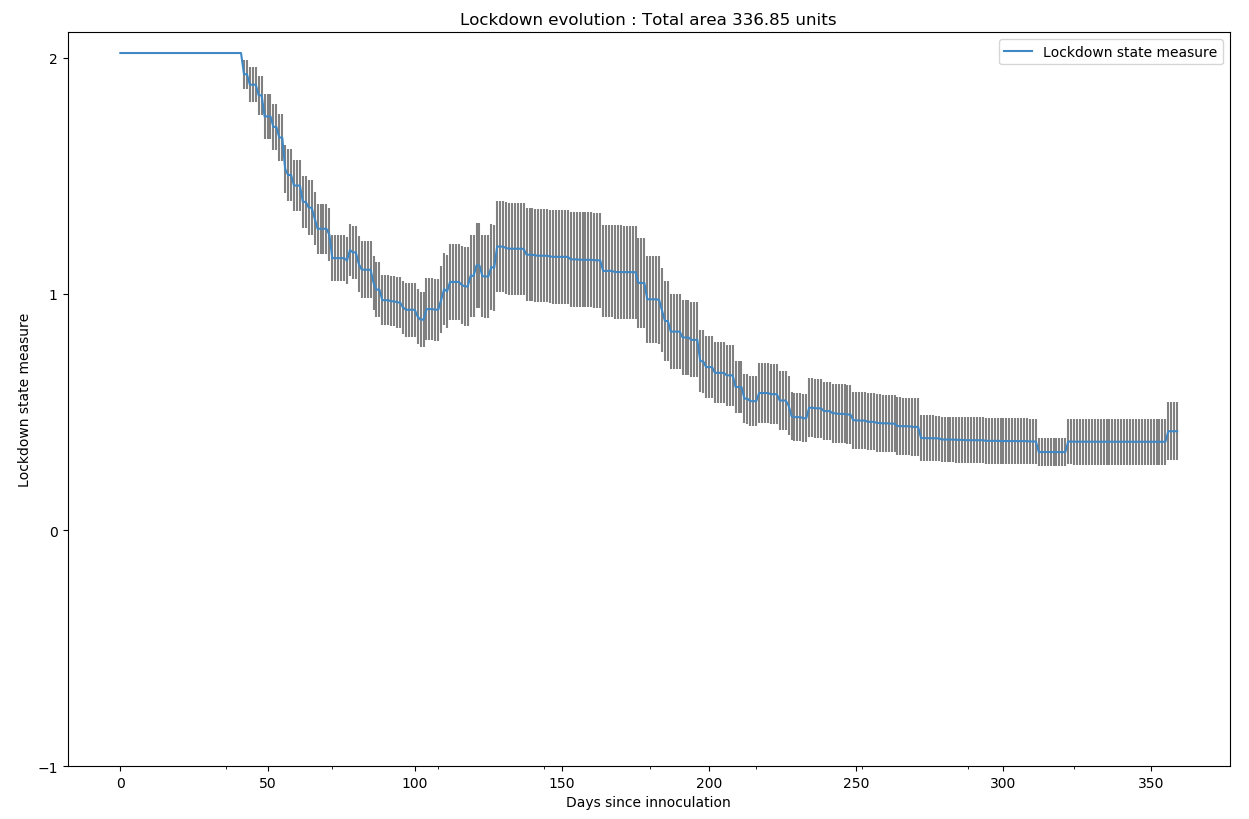
Lorsqu’on regarde la courbe d’évolution de la mesure de confinement, on constate un rebond vers 150 jours correspondant probablement aux simulations où il fallu donner un tour de vis avant l’explosion.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 2 --extra 14 1 2 --imm 60 90   --draw exa pop summ lock hos new R0

Scénario 3 - L’immunité collective : Ce scénario paraît irréaliste dans le cas d’une immunité temporaire. Mais nous allons constater des phénomènes intrigants :

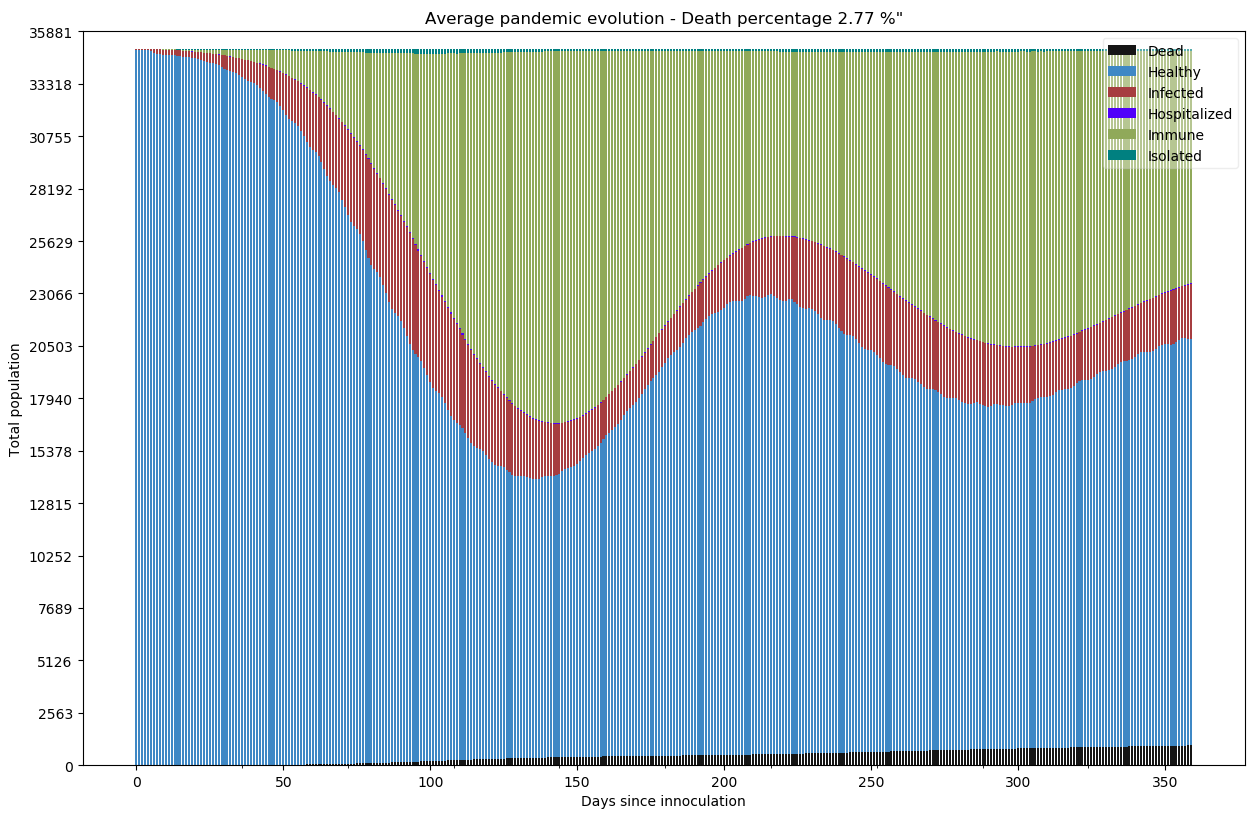
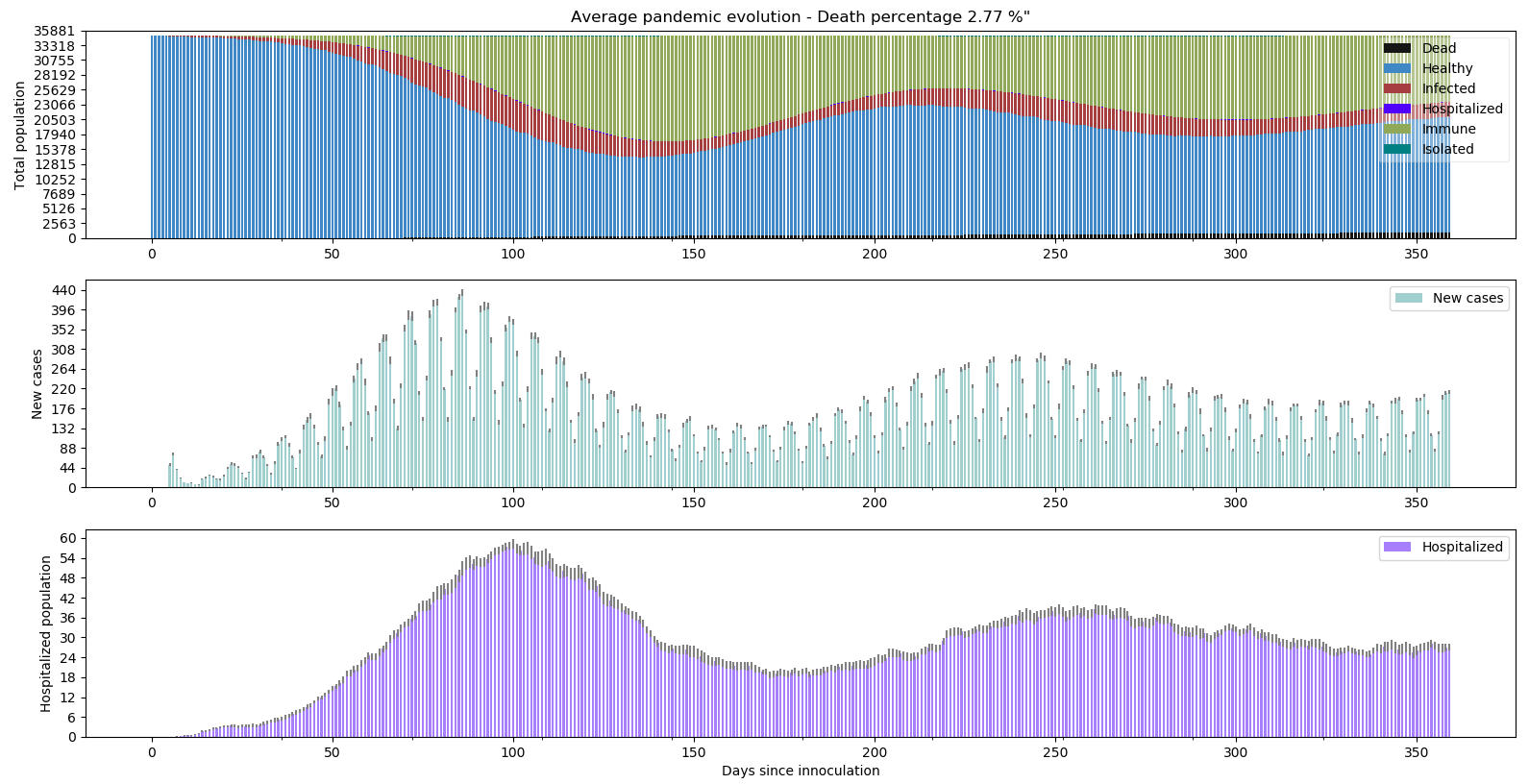
Un phénomène de vague d’infection empêche l’immunité collective et reverse des immunisés dans les personnes saines pouvant être contaminées. Lorsque le nombre d’immunisé augmente, la pandémie ralentit naturellement. Mais dès que l’immunité disparaît, la pandémie profite du vivier de personnes saines plus important pour se propager. Peut-on faire un parallèle avec les épisodes de grippes saisonnière dont on sait que l’immunité plus ou moins temporaire empêche le développement d’un vaccin stable ? Seul un épidémiologiste saurait à priori répondre.

Constatons simplement que nous atteignons ainsi déjà 2.77% de mortalité et ce pourcentage ne peut que croître tant que les vagues ne se sont pas stabilisées.

python -m scenario.run --nrun 20  --nday 360 --nind 35000 --scenario 3 --extra 0 --imm 60 90  --draw exa pop summ hos new

Enfin, nous terminerons sur une note négative :
Scénario X - La grippe saisonnière : La pire situation possible. Aucune précaution sociétale ou individuelle n’est prise. L’infection au virus ne donne qu’une courte immunité de 1 à 3 mois. Combien faut-il de temps pour décimer la population ?

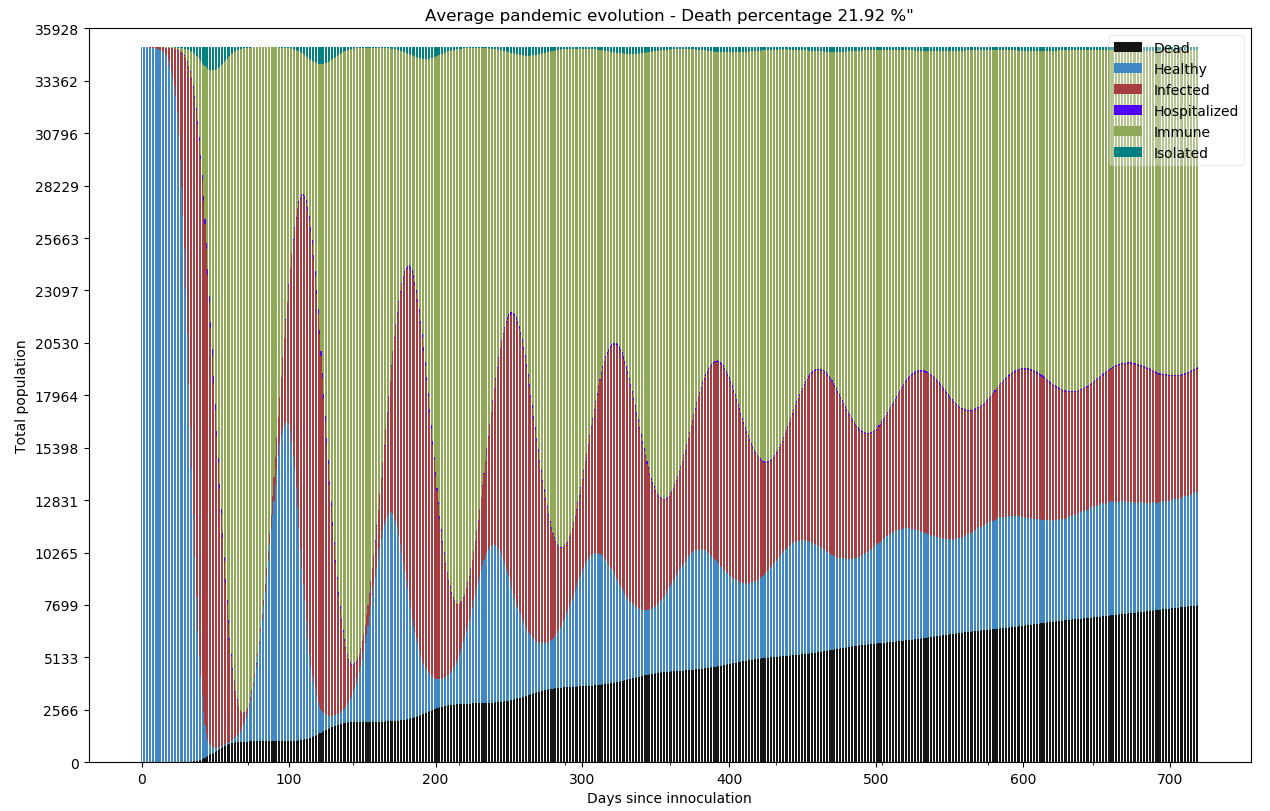
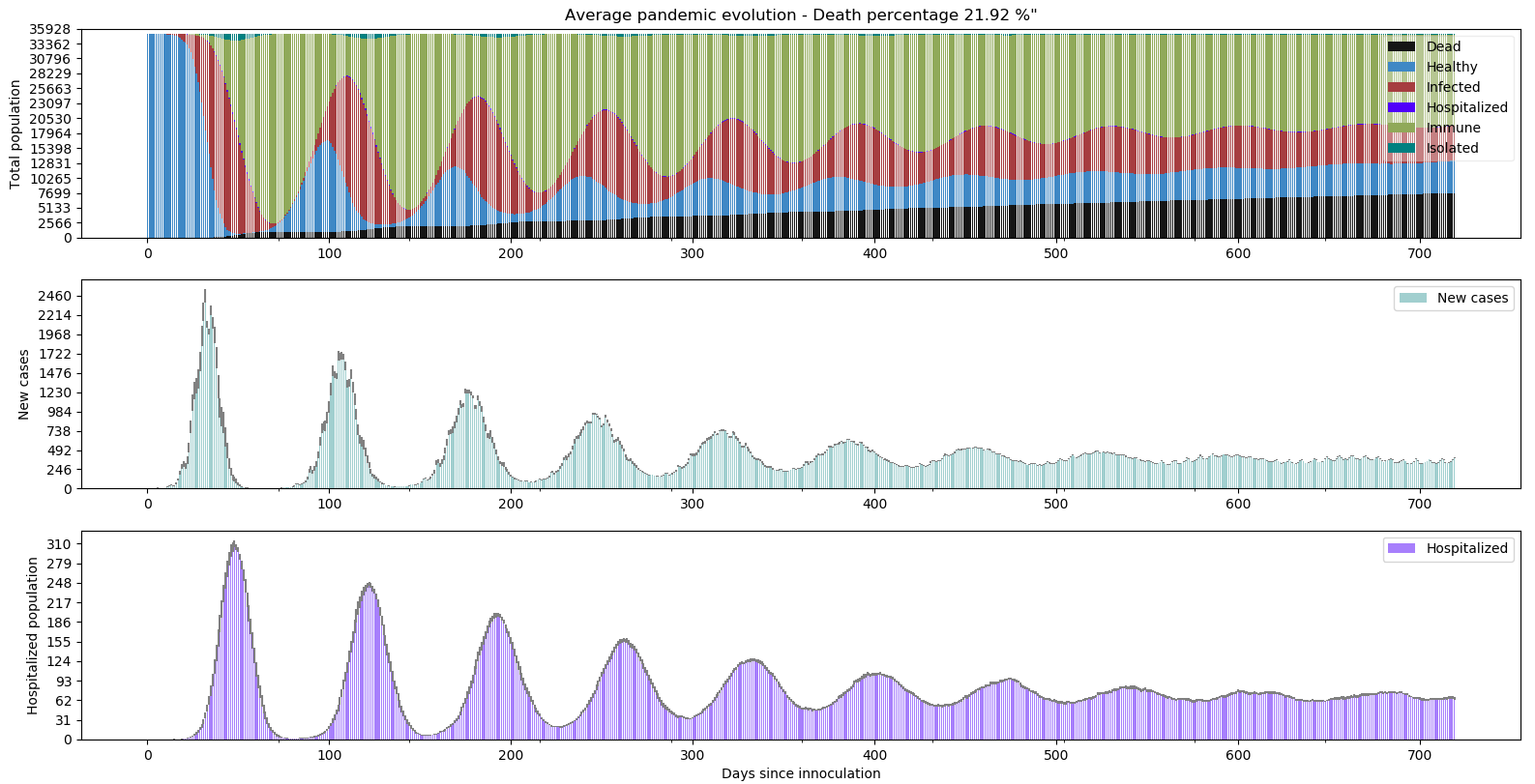
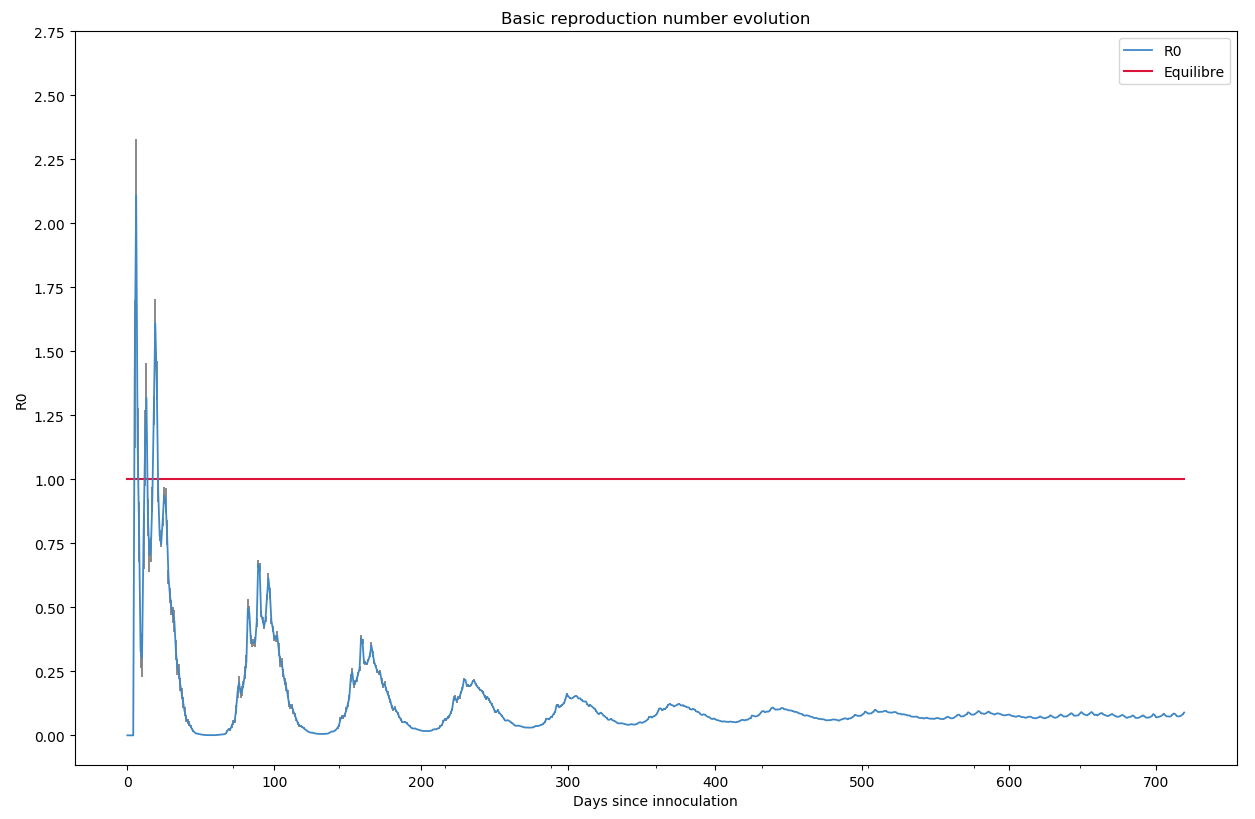
Vous connaissez maintenant suffisamment bien les graphiques pour les analysez vous-même.

python -m scenario.run --nrun 20  --nday 720 --nind 35000 --scenario -1 --imm 30 60  --draw exa pop summ R0

Takeaway scénario 7

Etant donné la contagiosité du Covid-19 et son taux de mortalité relativement élevé comparé à des virus similaires, une immunité temporaire serait une très mauvaise nouvelle pour notre civilisation à moyen terme et nous imposera de repenser encore plus profondément qu’aujourd’hui le fonctionnement de l’humanité.

D’autres scénarios ?

• Déconfiner uniquement les plus jeunes et inviter les plus âgés à rester chez eux. Mais dans ce cas, comment empêcher les contaminations dans les maisons. Nos parents et grand-parents ne sont pas enfermés dans des établissements comme beaucoup d’autres pays. Rien d’intéressant ne sortirait de ce scénario avec notre modélisation (qui se veut quelque part refléter la société)
• Le scénario des tests massifs aurait pu être testé en isolant automatiquement par exemple 5% de tous les infectés chaque jour. C’est simple à implémenter dans notre modèle mais irréaliste en pratique. Notre pays connaît un nombre de cas faible par rapport à d’autres et cela n’aurait pas de sens d’aller chercher des gens au hasard et les tester. J’ai donc inclu dans tous les scénario l’isolation de la famille car elle est logique et appliquée aujourd’hui chez nous
• Vous avez une idée ?

Revenir à l’index

Remarques méthodologiques

A propos des probabilités de contagion :

• Il est difficile de retro-engineerer des probabilités de contagion à partir de données macro comme le nombre de cas ou de décès que nous avons par les sources officielles. Tout ce que j’ai pu faire c’est chercher des valeurs qui me semblaient vraisemblables et qui offraient un comportement macro similaire à ce que j’imagine. Il y a donc un biais de sélection dans le choix des paramètres que j’ai essayé de modérer en restant consistant sur l’ensemble des scénarios (avec les paramètres de non-confinement, confinement naturel et confinement strict)

A propos de la projection de ces résultats sur la réalité :

• Difficile de se prononcer. Je préfère me tenir à l’aspect pédagogique de cet article. J’ai pris soin de tester unitairement l’ensemble des fonctions de propagations utilisées ce qui me donne confiance en les résultats de la modélisation (et j’invite les développeurs python à aller jeter un coup d’oeil). Mais comme dit auparavant, mon choix des paramètres n’a pas obéi à une approche empirique suffisamment robuste et la scalabilité à 35 millions d’individus nécessiterait plus de temps et d’infrastructure. Et probablement une réécriture du code. Je ferai cet exercice pour le plaisir de tester mes limites techniques mais je ne pense pas que les résultats changeront significativement

A propos de la taille des entreprises (à partir des données HCP) :

• Elles ne sont pas proportionnelles à la taille de l’échantillon ce qui fait qu’elles sont disproportionnellement plus grandes qu’elles ne devraient être. Mais il était nécessaire d’avoir des entreprises à plusieurs dizaines d’individus pour voir émerger les phénomènes de foyers sur les lieux de travail

Revenir à l’index

Prochaines étapes

• Elargir les simulations au million d’individus
• Modéliser le système scolaire et tester des scénarios d’ouverture progressive des écoles et universités
• Une visualisation interactive individuelle journalière à la manière de la vidéo de 3Blue1Brown
• Un jeu de paramètre pour chaque grande ville du pays
• Simuler une densité de population (promiscuité) et permettre au personnes “au mauvais comportement” d’aller dans des maisons voisines
• Utiliser la pyramide des âges marocaines au lieu de la pyramide mondiale
• Un scénario de tests aléatoires dans la population
• Un scénario d’isolation massive de zones géographiques ou de quartiers si par exemple plus 3 contamination ont lieu le même jour dans une zone géographique
• Un délai incompressible entre le test d’une personne et son isolation (les tests PCR peuvent prendre près d’une journée si les laboratoires sont surchargés)
• Un stock de tests maximum par jour (typiquement 4000 par jour pour la population marocaine en ce moment soit 4 tests par jour pour les 35k individus)
• L’isolation automatique d’un pourcentage des personnes qui travaillent au même endroit qu’une personne hospitalisée (de la même manière que c’est fait pour la famille)
• Modifier la définition du R0 pour passer d’un R0 journalier à un R0 sur la vie d’un individu (plus proche de la définition du R0 d’une épidémie)
• Simuler des individus spéciaux qui peuvent se déplacer dans n’importe quelle maison, épicerie ou lieu de travail (forces de l’ordre, médecins, responsables administratifs)

Le code est disponible, publique et les simulations reproduisibles

Vous retrouverez l’ensemble du code à jour ici (une simulation prend en moyenne 15 secondes et peut aller jusqu’à 20 minutes lorsqu’on allonge l’horizon temporel) :

https://github.com/AshtonIzmev/covid-19-pandemic-simulation

Mises à jour

L’article sera mis à jour au fur et à mesure de vos retours ou nouvelles idées

• 02/05/2020 : Ajout d’une section next steps

Remerciements

• Tous ceux qui ont proposé des idées, suggestions, encouragements et réflexions sur l’article précédent sur le Covid-19
• Abdelmouise pour sa contribution au code
• Mohamed pour la suggestion d’une loi normale pour le nombre d’individu par foyer au Maroc (à partir des données HCP)

Sources

[1] WHO Investigates Reports of Recovered COVID-19 Patients Testing Positive Again https://www.sciencealert.com/who-investigates-reports-of-recovered-covid-19-patients-testing-positive-again
[2] Recovered coronavirus patients are testing positive again. Can you get reinfected? https://edition.cnn.com/2020/04/17/health/south-korea-coronavirus-retesting-positive-intl-hnk/index.html
[3] Updated understanding of the outbreak of 2019 novel coronavirus (2019‐nCoV) in Wuhan, China https://onlinelibrary.wiley.com/doi/full/10.1002/jmv.25689?af=R
[5] The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application https://annals.org/aim/fullarticle/2762808/incubation-period-coronavirus-disease-2019-covid-19-from-publicly-reported
[6] Age, Sex, Existing Conditions of COVID-19 Cases and Deaths https://www.worldometers.info/coronavirus/coronavirus-age-sex-demographics/
[7] COVID-19 Laboratory-Confirmed Hospitalizations https://gis.cdc.gov/grasp/COVIDNet/COVID19_5.html
[8] Population Pyramids of the World from 1950 to 2100 https://www.populationpyramid.net/world/2019/
[9] Coronavirus seems to mutate much slower than seasonal flu https://www.livescience.com/coronavirus-mutation-rate.html
[10] Le trilemme du déconfinement, ou comment résoudre un problème insoluble https://www.linkedin.com/pulse/le-trilemme-du-d%C3%A9confinement-ou-comment-r%C3%A9soudre-un-probl%C3%A8me-sibony/
[11] LES PRINCIPALES CARACTÉRISTIQUES DE LA POPULATION ACTIVE OCCUPÉE EN 2019 https://www.hcp.ma/Les-principales-caracteristiques-de-la-population-active-occupee-en-2019_a2463.html
[12] Recensement Général de la Population et de l’Habitat 2014 : Microdonnées anonymisées https://www.hcp.ma/Open-Data_a2401.html
[13] COVID-19 : Morocco Expands Hospital Capacity http://northafricapost.com/39786-covid-19-morocco-expands-hospital-capacity.html
[14] US anti-lockdown rallies could cause surge in Covid-19 cases, experts warn https://www.theguardian.com/us-news/2020/apr/20/us-protests-lockdown-coronavirus-cases-surge-warning
[15] Twitter : Le 18ème vient officiellement de s’auto-déconfiner (et il aimerait qu’on le laisse danser) https://twitter.com/CocoChrist/status/1254125416421437440
[16] Covid-19 : la bourse ou la vie ? Sur l’inanité de la science économique officielle https://www.contretemps.eu/economie-covid19/
[17] Swedish Ambassador Says Stockholm Expected To Reach ‘Herd Immunity’ In May https://www.npr.org/2020/04/26/845211085/stockholm-expected-to-reach-herd-immunity-in-may-swedish-ambassador-says
[18] Wikipedia : List of countries by hospital beds https://en.wikipedia.org/wiki/List_of_countries_by_hospital_beds
[19] How an Austrian ski resort helped coronavirus spread across Europe https://edition.cnn.com/2020/03/24/europe/austria-ski-resort-ischgl-coronavirus-intl/index.html
[20] India quarantines 15,000 after ‘super-spreader’ dies of virus https://www.aljazeera.com/news/2020/03/india-quarantines-15000-virus-kills-super-spreader-guru-200328092832309.html
[21] (daté du 2 avril) هذه أجواء سوق المدينة القديمة في زمن كورونا https://www.youtube.com/watch?v=L49n6637pXQ
[22] Pour la « Golden week » en Chine, le tourisme s’éveille prudemment https://www.la-croix.com/Monde/Asie-et-Oceanie/Golden-week-Chine-tourisme-seveille-prudemment-2020-05-01-1201092075
[23] TRUMP’S DEADLY MISTAKE IN COMPARING CORONAVIRUS TO FLU https://theintercept.com/2020/03/25/coronavirus-flu-comparison-trump/

Revenir à l’index