Une simulation de pandémie à échelle individuelle (inspirée par le Covid-19 au Maroc)

Face à l’expansion du Covid-19 partout dans le monde, il est difficile de rester confiné chez soi sans tenter de mieux comprendre comment fonctionne et évolue la propagation d’une pandémie aussi foudroyante, menottant nos libertés et mettant à genoux nos économies.

Mais ce n’est pas ce qui m’a principalement motivé à écrire cet article et réaliser les simulations plus bas… J’ai en effet pu constater un afflux de publications d’articles dans de grands journaux électroniques (Medias24 et LeDesk pour ne citer qu’eux) faisant la promotion du travail de datascientists essayant de prédire notamment la fin de la pandémie dans notre pays.

Une épidémie est un sujet complexe

Je ne remets pas en cause l’effort réalisé par ces personnes pour essayer d’apporter une meilleure compréhension de la propagation de ce coronavirus chez nos concitoyens ainsi que chez les pouvoirs publics. Je veux cependant avertir des points suivants :

• L’évolution d’une pandémie est extrêmement difficile à prédire car elle est liée à un grand nombre de facteurs de la vie individuelle de chacun dont personne ne possède quasiment aucune information, à fortiori un datascientist
• Cette évolution est également liée à de nécessaires politiques de restriction de libertés telles un confinement de population, l’obligation de porter des masques ou encore l’interdiction des manifestations publiques. Ces macro-paramètres influencent fortement le déroulement de l’épidémie et sont difficiles à modéliser sans un travail de fond préalable basé sur des pandémies précédentes
• Etant donné la multiplicité des facteurs entrant en compte dans une pandémie, le plus simple est de l’attaquer par une approche stochastique avec des probabilités à tour de bras
• Comme une pandémie concerne un très grand nombre de personnes, simuler stochastiquement la vie de chacun est quasi impossible, ce qui nous force à utiliser des modèles épidémiologiques qui décrivent l’évolution de la pandémie. On va généralement s’intéresser à l’évolution du nombre de personnes infectées ou nombre de personnes décédées et essayer de prédire ces évolutions en utilisant un ensemble d’équations

Au regard de ces 4 points, il apparaît que la prédiction d’une pandémie de cette nature appartient bien plus au domaine des statistiques qu’à la datascience qui est aujourd’hui une sorte de fourre-tout méthodologique dont l’idée principale est d’extraire de l’information (ici de la prédiction) sur la base d’un nombre important de variables non contrôlées souvent fortement bruitées issues d’une proportion non négligeable d’observations, le tout permettant un relâchement méthodologique bien venu.

Il ne me semble pas aujourd’hui que la problématique de prédire la fin de la pandémie du Covid-19 ou le nombre global de personnes ayant été infectées soit un sujet de datascience. Il mérite donc bien plus de précaution.

Soyons responsables

Mais ce n’est pas la seule raison qui me pousse à commenter ces démarches scientifiques publiques

• Une pandémie est un sujet sérieux dans lequel le moindre risque de manipulation d’opinion doit être sujet à une éthique irréprochable. Un datascientist est dans les médias encore dépositaire d’une forme de magie noire mal comprise des profanes. Cela donne une crédibilité dont il faut user avec discernement
• Il faut agir avec responsabilité. Si vous pensez que la pandémie va s’arrêter le X avril, ne le dites qu’avec un maximum de précaution (en statistique, nous avons par exemple des intervalles de confiance) et prévenez le journaliste heureux dépositaire de votre scoop de prendre l’ensemble des précautions de langage nécessaires. Autrement, si vous vous trompez, et statistiquement il est sûr que vous vous trompez, vous poussez les gens à réduire l’effort déjà difficile de confinement et nuisez aux politiques publiques mises en place
• Publiez votre code. Il n’y a aucun scientifique au monde qui ne fera une déclaration sans publier de manière exhaustive et reproductible son code et la donnée sur laquelle il se base. Il n’y a pas de crédibilité sans une transparence complète. Cela permet aux collègues et spécialistes de participer dans une démarche d’amélioration et de recherche de la vérité (statistique)

Une contribution

Le personnel médical est au front de cette guerre, les autorités ajustent tant bien que mal leur politiques de santé publique, les intellectuels pensent le futur de nos sociétés meurtries et nous autres informaticiens et amoureux de la data modélisons. Chacun ses armes.

De la simple modélisation de distribution gaussienne (ce qui ne semble pas avoir de fondement théorique sinon d’approximer le phénomène par le théorème centrale limite ce qui semble simpliste, voir ce thread de stats.stackexchange.com Is the covid-19 pandemic curve a gaussian curve) jusqu’aux modélisations SIR et SIER Wikipedia / Elaborations on the basic SIR model, il y a tout un monde épidémiologique qu’il est passionnant d’explorer.

J’ai pour ma part choisi d’adopter une démarche un peu différente de ce que l’on voit autour de nous, à savoir de modéliser le comportement à l’échelle individuelle : la maison, l’épicerie, le lieu de travail etc.

Hypothèses de base

Une pandémie est déclenchée par deux éléments

• Un ensemble N d’individus répartis géographiquement dont un certain pourcentage est initialement porteur du virus
• Des lieux de rencontre pour la transmission du virus :
  • Les foyers familiaux dans lesquels tous les occupants sont fortement exposés
  • Les épiceries qui connaissent un afflux important d’individus de foyers divers
  • Les lieux de travail dans lesquels nous passons un certain temps avec une population bien définie

A partir de cette simple modélisation de la vie, nous appliquons quelques règles de confinement simple :

• Un seule personne va à l’épicerie une fois par jour
• Un pourcentage défini de la population adulte est en télé-travail
• Il n’y a pas de contamination dans les transports publiques ni dans les cafés, restaurants etc.

Le confinement simplifie en quelques sorte nos vies et par conséquent nos modélisations.

Les paramètres choisis

Nous simulons 5000 individus sur une période de 120 jours. Nous avons ajusté les foyers pour avoir à peu près 3.5 individus par foyer et avons choisi d’estimer qu’il y a 1 épicerie pour 20 foyers. La probabilité journalière d’être infecté est de 50% à la maison (en raison de la promiscuité), 5% à l’épicerie (on n’y passe pas beaucoup de temps) et de 10% au travail. On assigne à chaque foyer l’épicerie la plus proche de sa résidence. Les entreprises sont constituées de 44% d’entreprises de moins de 3 employés (TPE), de 42% d’entreprises de moins de 15 employés (PME) et de 14% d’entreprises de moins de 50 employés (GE). Les enfants ne vont pas à l’école ni à l’épicerie, ni à fortiori au travail. Une seule personne adulte par foyer va à l’épicerie une fois par jour. Chaque foyer est constitué aléatoirement d’individus suivant une pyramide d’âge classique. Le taux de mortalité du virus suit les covid-19 mortality rate mondiaux. Le virus est contagieux entre 2 et 7 jours après l’infection, et la décision mort ou immunité dépend de l’âge et se décide au bout de 21 à 39 jours après infection. Un individu mort ou immunisé n’est évidemment plus contagieux.

Tous ces paramètres peuvent être modifiés et ajustés. Ils correspondent grosso modo à ma compréhension d’une pandémie mais a une visée pédagogique et non prédictive.

Pourquoi simuler la vie de chacun alors que des modélisations macro existent ?

Disposer d’une simulation de chaque individu permet de contrôler plus naturellement les paramètres de cette pandémie. La raison originelle pour cette expérience était la volonté de connaître l’impact d’un déconfinement progressif sur la pandémie, à travers un relâchement du port des masques et un retour au travail. Je voulais également distinguer les souks qui propagent plus rapidement la maladie des épiceries et grandes surfaces normales.

Alors quels sont les résultats ?

Disclaimer : Tous les résultats donnés ici ne servent qu’à illustrer une pandémie virale et pas à donner des prédictions sur la situation actuelle. Je laisse ce travail aux épidémiologistes et scientifiques qui ont consacré leurs vies à modéliser ces phénomènes.

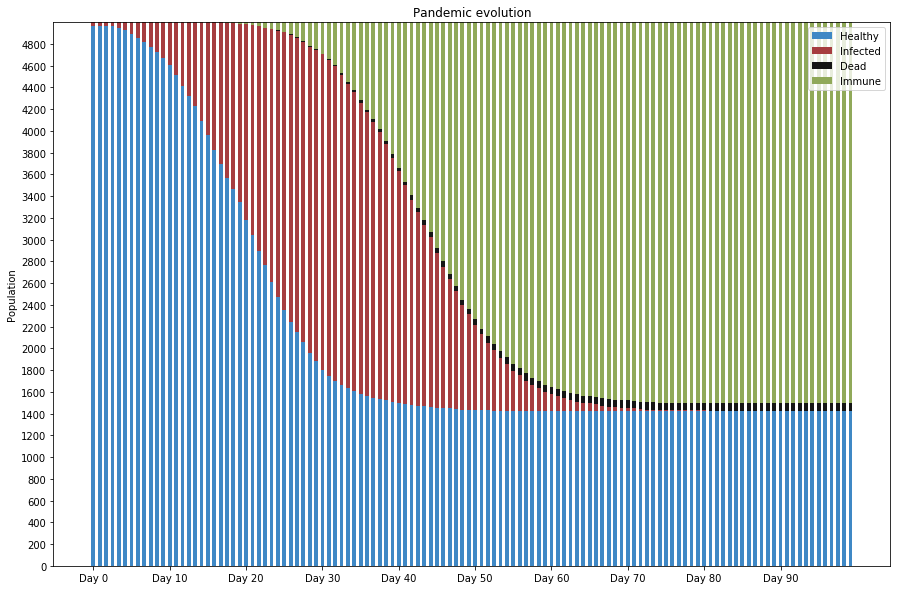
Voici la courbe qui décrit l’état de la population sur les 120 jours à partir d’une inoculation initiale du virus sur 0.5% de la population. 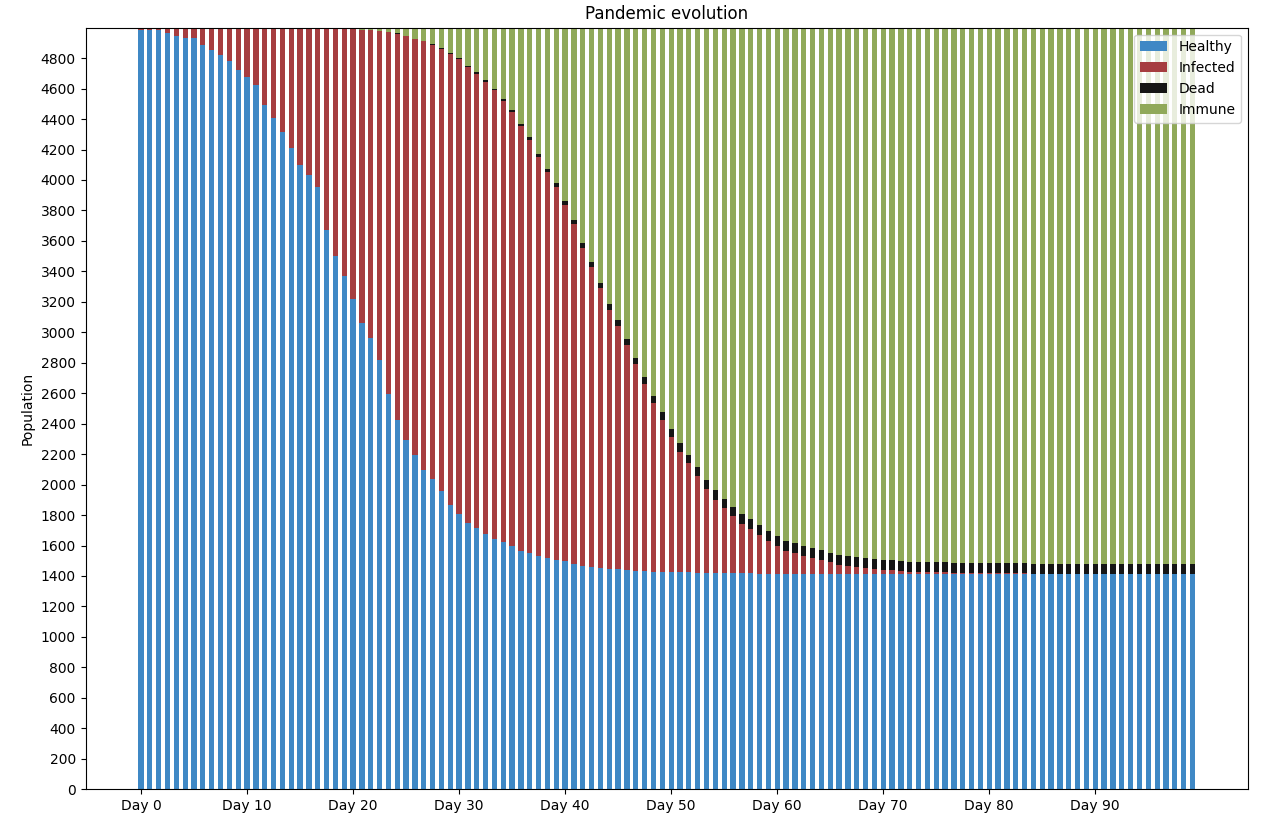Chaque barre représente l’état de la population à un jour donné. En bleu les personnes saines, en rouge les personnes infectées (qui transitionnent vers la mort ou l’immunité), en noir les personnes décédées et en vert les personnes immunisées. L’information importante à retenir ici est la forme de l’évolution de la transition de la sanité vers l’immunité ainsi que le pourcentage de personnes saines jamais infectées en fin de pandémie.

Il est intéressant de voir la pandémie s’arrêter lorsqu’un pourcentage spécifique de la population est infectée (herd immunity). Lorsqu’un confinement sévère est appliqué, le taux de reproduction du virus est fortement diminué et la pandémie s’éteint car il y a beaucoup d’individus immunisés.

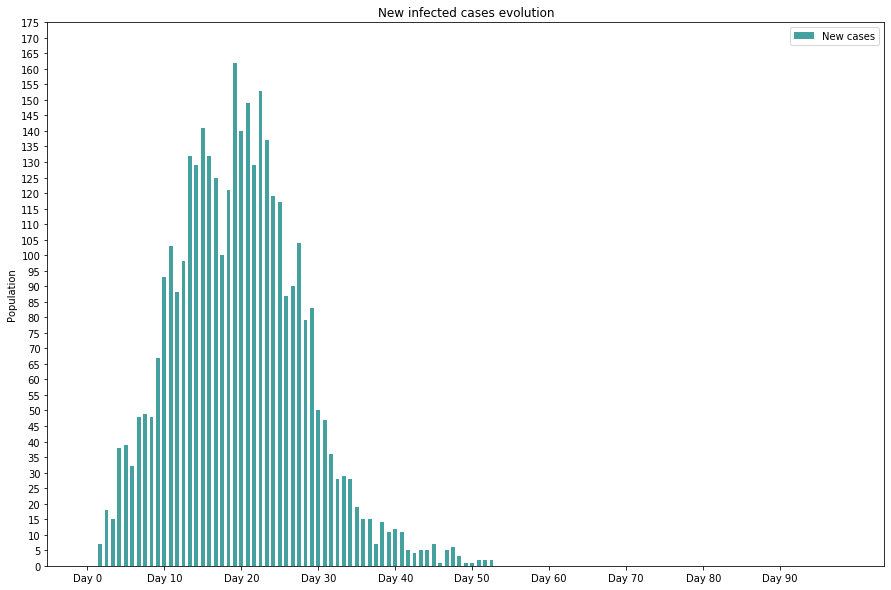
Voici la courbe qui décrit l’augmentation de nouveaux cas chaque jour 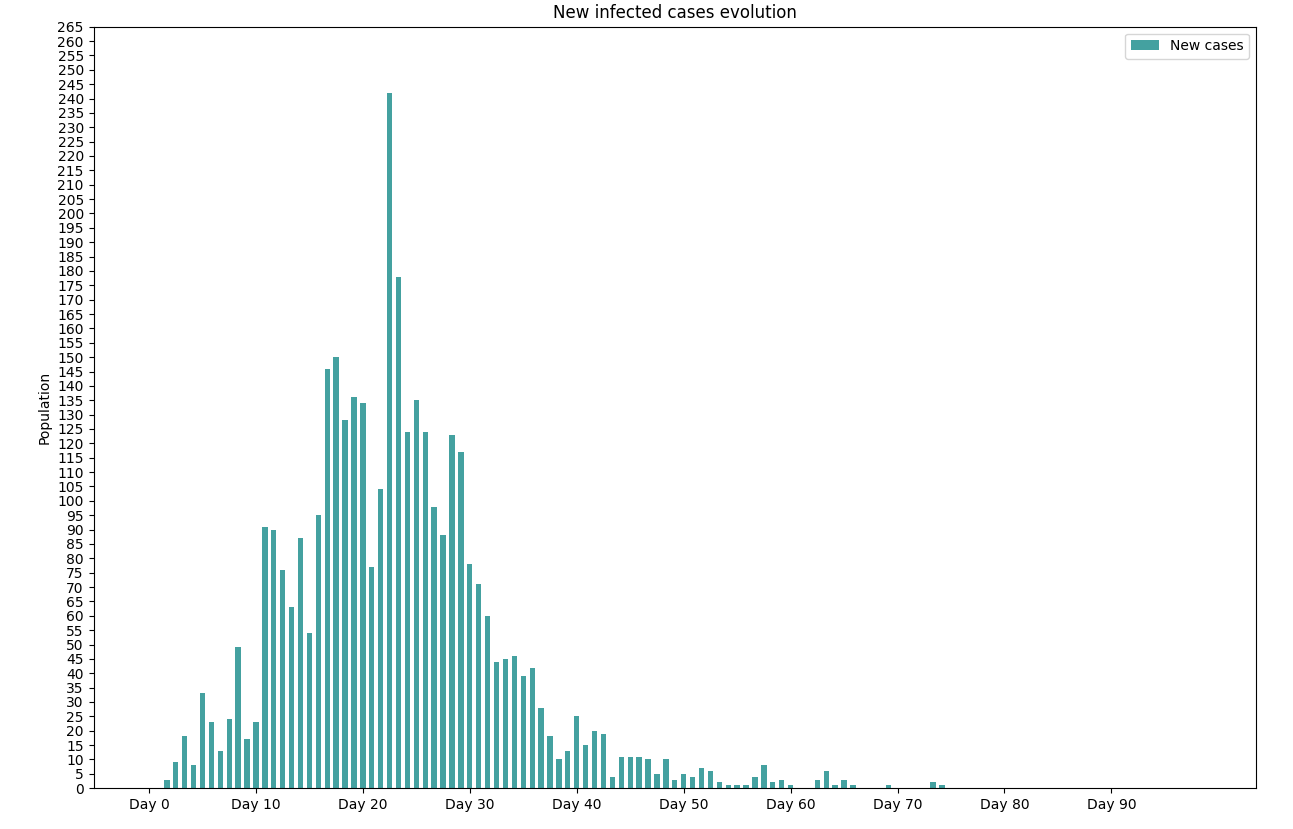Je trouve intéressant de constater que l’histogramme a une long tail (c’est-à-dire des occurences d’infection éloignées du pic Wikipedia/Long_tail) : le virus subsiste et a de plus en plus de mal à se propager mais cette propagation s’éteint plus lentement qu’on ne pourrait le pressentir. Cette long tail me semble être un vrai danger car elle peut donner l’illusion que la pandémie est finie alors qu’elle peut repartir si le confinement est relâché (ce qu’on pourrait simuler en supprimant le télé-travail dans notre modélisation par exemple).

Prochaines étapes

1. Modéliser le transport public
2. Étudier des scénarios de relâchement de confinement à quelques jours de la fin de la pandémie (pour voir les résurgences)
3. Ajouter l’hospitalisation dans les états possible d’un individu (il n’est alors plus contagieux)
4. Ouvrir la voie à d’autres types de contamination (marcher dans la rue, aller à l’hopital etc.)
5. Modéliser une immunité temporaire ou supprimer l’immunité qui n’est pas prouvée
6. Faire varier le niveau de confinement selon les zones géographiques et quartiers

(Merci à tous ceux qui m’ont fait parvenir leurs suggestions)

Le code est disponible, publique et reproduisible

Vous retrouverez l’ensemble du code à jour ici github.com/AshtonIzmev/covid-19-pandemic-simulation. J’invite toute personne suffisamment motivée à reprendre le code, le critiquer et à l’adapter à notre contexte pour éventuellement en tirer les conclusions qui s’imposeraient avec les précautions d’usage.

Ci-bas une version simplifiée (le code structuré selon les standards d’usage est sur github) et lisible au format notebook au 11/04/2020 :

Bonne lecture pour les plus courageux

import pandas as pd
import numpy as np
from scipy import spatial
import random as rand
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Markdown as md

N=5000 # number of people
N_days = 120 # Number of simulated days
NB_STO_PER_HOU = 20 # Let's say we have 20 houses for each grocerie store
PROBA_SAME_HOUSE_RATE = 10/100 # probability used to set the number of person per house
PROB_INFECTION_AT_HOME = 0.5 # Probabilty of infecting a random family member (same house)
PROB_INFECTION_AT_WORK = 0.1 # Probabilty of infecting a random co-worker
PROB_INFECTION_AT_STORE = 0.05 # Probabilty of infecting someone who goes to the same store
TPE_MAX_EMPLOYEES = 3
PME_MAX_EMPLOYEES = 15
GE_MAX_EMPLOYEES = 50
DISPLAY = False

IMMUNE_STATE = -2
HEALTHY_STATE = -1
DEAD_STATE = 0

flatten = lambda l: [item for sublist in l for item in sublist]

def getR():
    return rand.random()

def lazyRChoice(ll):
    for l in ll:
        if len(l) > 0:
            yield rand.choice(l)

def getInfectionParameters():
    return int(21+ (39-21)*getR()), int(2+ (7-2)*getR()) # Time to death/immunity , Time to contagiosity

def updateInfectionPeriod(who_is_infected, incubation_dic, contagion_dic):
    for i in who_is_infected:
        if incubation_dic[i] == HEALTHY_STATE: # If has never been infected
            incubation, contagion = getInfectionParameters()
            incubation_dic[i] = incubation
            contagion_dic[i] = contagion

We gather a mortality rate by age (ten year increments)

# Source : https://www.worldometers.info/coronavirus/coronavirus-age-sex-demographics/
mortality_rate = {
    8: 0.148, 
    7: 0.08, 
    6: 0.036, 
    5: 0.013, # 50-59 yo => 0.013 probability of dying
    4: 0.04, 
    3: 0.02, 
    2: 0.02, 
    1: 0.02, 
    0: 0
}

def getMortaltyRate(age):
    i = next(x for x in enumerate(list(mortality_rate.keys())) if x[1] <= age/10)
    return  mortality_rate[i[1]]

def getInfectedPeople(incubation_dic):
    return [k for k,v in incubation_dic.items() if v > DEAD_STATE]

def getDeadPeople(incubation_dic):
    return [k for k,v in incubation_dic.items() if v == DEAD_STATE]

def getHealthyPeople(incubation_dic):
    return [k for k,v in incubation_dic.items() if v == HEALTHY_STATE]

def getImmunePeople(incubation_dic):
    return [k for k,v in incubation_dic.items() if v == IMMUNE_STATE]

def incrementInfectionDay(incubation_dic, age_dic, contagion_dic):
    for i in getInfectedPeople(incubation_dic):
        contagion_dic[i] = contagion_dic[i] -1
        if incubation_dic[i] > DEAD_STATE + 1:
            incubation_dic[i] = incubation_dic[i] -1
        if incubation_dic[i] == DEAD_STATE + 1: # Decide over life
            if getR() < getMortaltyRate(age_dic[i]):
                incubation_dic[i] = 0
            else:
                incubation_dic[i] = -2 # Grant immunity

def isContagious(ind, contagion_dic):
    return contagion_dic[ind] < 0

We will try to avoid O(n²) as much as possible, ideally O(n.log(n))

Let’s build a probability function to assign a coherent age to each individual

# Source https://www.populationpyramid.net/world/2019/
age_distribution = pd.DataFrame([
    ["0-4",349247348,328119059], 
    ["5-9",341670620,320090537],
    ["10-14",328942130,307203261], 
    ["15-19",314806147,293931999], 
    ["20-24",307809031,288834393], 
    ["25-29",307548367,290783757], 
    ["30-34",305762271,293702434], 
    ["35-39",270507560,262936512], 
    ["40-44",247594384,242696599], 
    ["45-49",239897308,237022350], 
    ["50-54",218833001,219504648], 
    ["55-59",187135108,190624979], 
    ["60-64",153758680,161570707], 
    ["65-69",124471230,136004171], 
    ["70-74",82793263,96515002], 
    ["75-79",53073892,66973202], 
    ["80-84",33071682,47305811], 
    ["85-89",15423679,25733670], 
    ["90-94",5370654,11222622], 
    ["95-99",1203726,3239297], 
    ["100-125",114528,418582]], columns=['age', 'nb_men', 'nb_women'])
age_distribution['nb'] = age_distribution['nb_men'] + age_distribution['nb_women']
age_distribution['pct'] = age_distribution['nb'] / age_distribution['nb'].sum()
age_distribution['min_age'] = age_distribution['age'].map(lambda s:int(s.split('-')[0]))
age_distribution['max_age'] = age_distribution['age'].map(lambda s:int(s.split('-')[1]))

We need to separate adults and children

# We did a cut to 25 years old for adult
age_distribution_children = age_distribution.iloc[:7]
age_distribution_adults = age_distribution.iloc[4:]

age_distribution_children

age_distribution_adults

Build cumulative distribution for age repartition

It will be used after house allocation

age_distribution_children_cumsum = \
    age_distribution_children['pct'].cumsum() / age_distribution_children['pct'].cumsum().max()
age_distribution_adults_cumsum = \
    age_distribution_adults['pct'].cumsum() / age_distribution_adults['pct'].cumsum().max()

This function is used to attribute an age given the range of our age data and the cumulative distribution

def getAge(isChild):
    if isChild:
        l_cs = age_distribution_children_cumsum
        l_dis = age_distribution_children
    else:
        l_cs = age_distribution_adults_cumsum
        l_dis = age_distribution_adults
    i = next(x[0] for x in enumerate(l_cs.values) if x[1] > getR())
    min_age_i = l_dis.iloc[i]['min_age']
    max_age_i = l_dis.iloc[i]['max_age']
    return int(min_age_i + (max_age_i-min_age_i)*getR())

We need to allocate individuals to houses

# Individual -> House
all_ind_hou = {}
i_hou = 0
i_ind = 0
is_first_person = True
prob_keep_hou = getR()
while i_ind < N :
    if is_first_person:
        all_ind_hou[i_ind] = i_hou # Attach first person to the house
        i_ind = i_ind + 1 # GOTO next person
        is_first_person = False
        continue
    if prob_keep_hou > PROBA_SAME_HOUSE_RATE:
        all_ind_hou[i_ind] = i_hou # Attach Next person
        i_ind = i_ind + 1 # GOTO next person
        prob_keep_hou = prob_keep_hou / 2 # Divide probability keep_foy
    else:
        i_hou = i_hou + 1 # GOTO next house
        prob_keep_hou = getR() # RESET keep_hou probability
        is_first_person = True # New house needs a first person

max(all_ind_hou.keys()), max(all_ind_hou.values())

And in a similar manner, we will allocate a list of people for each house (it will be handy)

# House -> List of individuals
all_hou_ind = {}
for k, v in all_ind_hou.items():
    all_hou_ind[v] = all_hou_ind.get(v, [])
    all_hou_ind[v].append(k)

The number of houses is then set when all individuals have a home

N_hou = i_hou+1 # Set the number of houses
N_sto = int(N_hou/NB_STO_PER_HOU) # Set the number of stores

md("There are %.2f individuals per house for a total of %d houses"%(
    pd.Series(all_ind_hou).value_counts().mean(), N_hou))

There are 3.52 individuals per house for a total of 1419 houses

Let’s allocate an age to each individual

At least one adult per house, and children start when at least 3 persons in a house

all_ind_adu = {} # We track who is adult to further affect a work
all_ind_age = {}
all_ind_age[0] = getAge(isChild=False)
all_ind_adu[0] = 1
incr_ind = 1
i_ind = 1
while i_ind < N:
    if all_ind_hou[i_ind] != all_ind_hou[i_ind-1]: # We have a new house
        incr_ind = 0
    if incr_ind < 2 :
        all_ind_age[i_ind] = getAge(isChild=False)
        all_ind_adu[i_ind] = 1
    else :
        all_ind_age[i_ind] = getAge(isChild=True)
        all_ind_adu[i_ind] = 0
    incr_ind = incr_ind + 1 
    i_ind = i_ind+1

Using the adult dictionnary, we can build a house -> adult map

# House -> List of adults (needed to check you goes to the store)
all_hou_adu = {}
for k, v in all_ind_hou.items():
    all_hou_adu[v] = [i for i in all_hou_adu.get(v, []) if all_ind_adu[i]==1]
    all_hou_adu[v].append(k)

Let’s check the result on the first few houses

pd.concat([pd.DataFrame(all_ind_age.values(), columns=['age']), 
           pd.DataFrame(all_ind_hou.values(), columns=['house_index'])], axis=1).head(15)

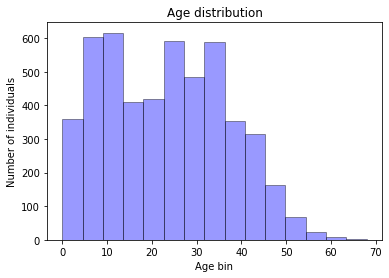
There are for sure side effects in the way I allocated age but its distribution still looks nice :)

# seaborn histogram
sns.distplot(list(all_ind_age.values()), hist=True, kde=False, 
             bins=15, color = 'blue',
             hist_kws={'edgecolor':'black'})
# Add labels
plt.title('Age distribution')
plt.xlabel('Age bin')
plt.ylabel('Number of individuals')

Text(0, 0.5, 'Number of individuals')

We set a geolocation point for every house and grocerie store

def getR2():
    u = getR()
    return 4*(u-0.5)*(u-0.5)*(u-0.5)+0.5

geo_hou = [ (getR(), getR()) for i in range(N_hou)]
geo_sto = [ (getR(), getR()) for i in range(N_sto)]

Let’s allocate a grocerie store for each house

I am begging you, do not reinvent the wheel…

distance, indexes = spatial.KDTree(geo_sto).query(geo_hou)

# House -> Grocerie store
all_hou_sto = dict(zip(range(N_hou), indexes))

# Grocerie store -> List of House
all_sto_hou = {}
for k, v in all_hou_sto.items():
    all_sto_hou[v] = all_sto_hou.get(v, [])
    all_sto_hou[v].append(k)

# Grocerie store -> List of Adults
all_sto_adu = {}
for k, v in all_hou_sto.items():
    all_sto_adu[v] = all_sto_adu.get(v, [])
    all_sto_adu[v].append(k)

md("There are %.2f individuals per house for a total of %d houses"%(
    pd.Series(all_ind_hou).value_counts().mean(), N_hou))

There are 3.52 individuals per house for a total of 1419 houses

Let’s finally choose a workplace for every individual

Let’s assume we have 44% of TPE, 42% of PME and 14% of GE in Morocco

Source : https://fnh.ma/article/actualite-economique/les-tpme-representent-93-des-entreprises-marocaines-en-2019

def pickWorkSize():
    p = getR()
    if p < 0.44:
        # We picked a TPE
        return int(1 + (TPE_MAX_EMPLOYEES-1)*getR())
    elif p < 0.86:
        # We picked a PME
        return int(TPE_MAX_EMPLOYEES + (PME_MAX_EMPLOYEES-TPE_MAX_EMPLOYEES)*getR())
    else:
        # We picked a PME
        return int(PME_MAX_EMPLOYEES + (GE_MAX_EMPLOYEES-PME_MAX_EMPLOYEES)*getR())

# Only adults work, and only half of them
workers = list([i for i in range(N) if getR() <0.5 and all_ind_adu[i]==1])
rand.shuffle(workers)
all_ind_wor = {}
i_ind = 0
i_wor = 0
while len(workers) > 0:
    for j in range(pickWorkSize()):
        if len(workers) == 0:
            break
        ind = workers.pop()
        all_ind_wor[ind] = i_wor
    i_wor = i_wor + 1

# workplace -> Individuals
all_wor_ind = {}
for k, v in all_ind_wor.items():
    all_wor_ind[v] = all_wor_ind.get(v, [])
    all_wor_ind[v].append(k)

N_wor = max(all_ind_wor.values()) # We set here the number of workplaces

md("There are %i workplaces in total"%(max(all_ind_wor.values())))

There are 171 workplaces in total

md("The %ith workplace has %i workers!!"%(
    pd.Series(all_ind_wor).value_counts().index[0], 
    pd.Series(all_ind_wor).value_counts().values[0]))

The 123th workplace has 49 workers!!

We set a geolocation point for every house and grocerie store

geo_wor = [ (getR2(), getR2()) for i in range(N_wor)]

Ok so let’s summarize all we’ve got before going to COVID simulation

md("There are %i individuals"%(N))

There are 5000 individuals

md("There are %i houses"%(N_hou))

There are 1419 houses

md("There are %i grocerie stores"%(N_sto))

There are 70 grocerie stores

md("There are %i workplaces"%(N_wor))

There are 171 workplaces

md("""Each individual has an age (which will be helpful later). Example: \n 
Person %i is %i years old \n
Person %i is %i years old etc..."""%(154, all_ind_age[154], 99, all_ind_age[99]))

Each individual has an age (which will be helpful later). Example:

Person 154 is 6 years old

Person 99 is 25 years old etc…

md("""Each individual is linked to a house. Example: \n 
Person %i lives in house %i \n
Person %i lives in house %i etc..."""%(17, all_ind_hou[17], 23, all_ind_hou[23]))

Each individual is linked to a house. Example:

Person 17 lives in house 4

Person 23 lives in house 6 etc…

md("""Each individual works at a company. Example: \n 
Person %i works at company %i \n
Person %i works at company %i etc..."""%(
    list(all_ind_wor.keys())[3], all_ind_wor[list(all_ind_wor.keys())[3]], 
    list(all_ind_wor.keys())[7], all_ind_wor[list(all_ind_wor.keys())[7]]))

Each individual works at a company. Example:

Person 3538 works at company 0

Person 2137 works at company 0 etc…

md("""Each house is linked to a grocerie store. Example: \n 
House %i is near store %i \n
House %i is near store %i etc..."""%(11, all_hou_sto[11], 27, all_hou_sto[27]))

Each house is linked to a grocerie store. Example:

House 11 is near store 44

House 27 is near store 67 etc…

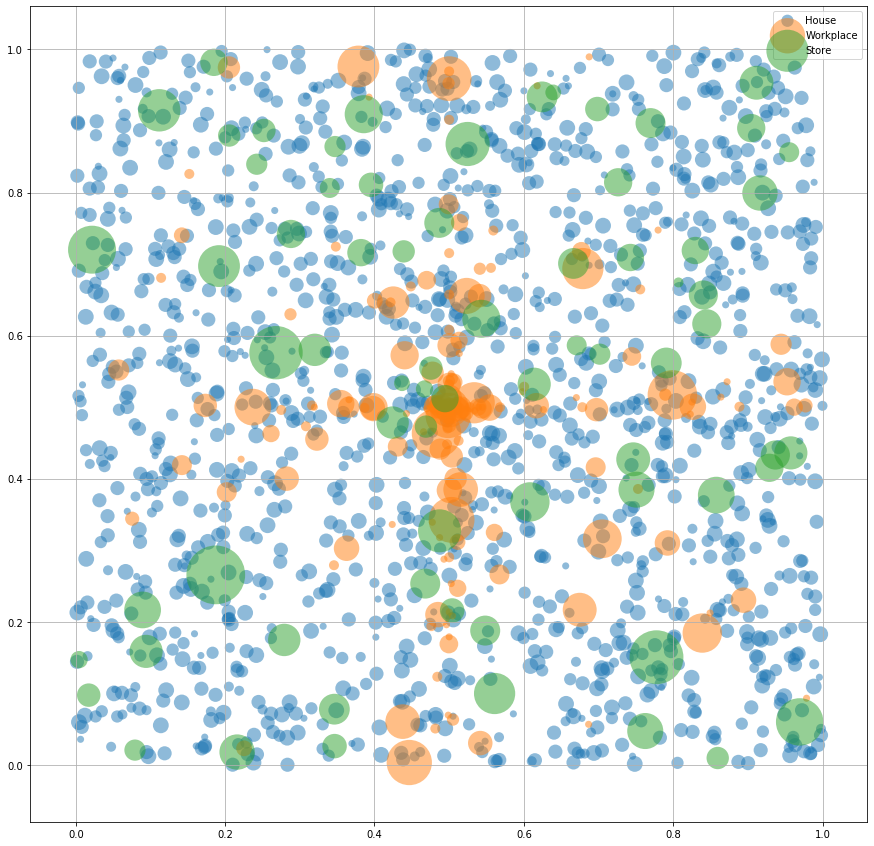
Ok, let’s visualize all this mess

Bubble sizes are the sum of individual (or houses) related to it

fig, ax = plt.subplots(figsize=(15, 15))
colors = ['tab:blue', 'tab:orange', 'tab:green']
    
scale_houses = 50*pd.Series(all_ind_hou).value_counts().sort_index().values # Size of each house
scale_workplaces = 50*pd.Series(all_ind_wor).value_counts().sort_index().values # Size of each house
scale_stores = 50*pd.Series(all_hou_sto).value_counts().sort_index().values # Size of each house

ax.scatter(np.array(geo_hou)[:,0], np.array(geo_hou)[:,1], c=colors[0], s=scale_houses, label="House", 
           alpha=0.5, edgecolors='none')
ax.scatter(np.array(geo_wor)[:,0], np.array(geo_wor)[:,1], c=colors[1], s=scale_workplaces, label="Workplace", 
           alpha=0.5, edgecolors='none')
ax.scatter(np.array(geo_sto)[:,0], np.array(geo_sto)[:,1], c=colors[2], s=scale_stores, label="Store", 
           alpha=0.5, edgecolors='none')

ax.legend()
ax.grid(True)

plt.show()

Propagation functions

Infection at home

def propagateToHouses(map_individuals_houses, map_houses_individuals, infection_state, contagion_state):
    # Houses that contain an infected and contagious person
    infected_houses = [map_individuals_houses[i] for i in getInfectedPeople(infection_state) 
                       if isContagious(i, contagion_state)]
    if DISPLAY:
        display(md("Which gives us %i infected different houses"%(len(infected_houses))))
    
    # People infected (not necessarily contagious) from a contagious person living in their house
    infected_athome = [i for i in flatten([map_houses_individuals[hou] for hou in infected_houses])
                            if getR() < PROB_INFECTION_AT_HOME]
    
    # INFECTION STATE UPDATE
    updateInfectionPeriod(infected_athome, infection_state, contagion_state)
    if DISPLAY:
        display(md("Ending at the morning with %i infected individuals"%(len(getInfectedPeople(infection_state)))))

def propagateToWorkplaces(map_individual_workers, map_workplace_individual, infection_state, contagion_state):
    # Contagious people who will go to work
    infected_gotowork = [i for i in getInfectedPeople(infection_state) if i in map_individual_workers.keys() 
                         and isContagious(i, contagion_state)]
    if DISPLAY:
        display(md("%i infected people go to work"%(len(infected_gotowork))))
        
    # Infected workplaces
    infected_workplaces = [map_individual_workers[ind] for ind in infected_gotowork]
    if DISPLAY:
        display(md("%i different work places are thus infected"%(len(infected_workplaces)))) 
    infected_backfromwork = [i for i in flatten([map_workplace_individual[k] for k in infected_workplaces]) 
                             if getR() < PROB_INFECTION_AT_WORK]
    
    # INFECTION STATE UPDATE
    updateInfectionPeriod(infected_backfromwork, infection_state, contagion_state)
    if DISPLAY:
        display(md("Ending at the morning with %i infected individuals"%(len(getInfectedPeople(infection_state)))))

def propagateToGroStores(map_individuals_houses, map_houses_stores, map_stores_houses, map_houses_adults, 
                         infection_state, contagion_state):
    # Filter on living people because we have a random choice to make in each house
    # People who will go to their store (one person per house as imposed by lockdown)
    individuals_gotostore = lazyRChoice([[i for i in map_houses_adults[h] if infection_state[i] != DEAD_STATE] 
                             for h in range(len(map_houses_adults))])
    if DISPLAY:
        display(md("In each house, a random adult goes to the store, which gives us %i individuals leaving"
               %(len(individuals_gotostore))))
    
    # Contagious people who will go to their store
    individuals_infected_gotostore = [i for i in individuals_gotostore if isContagious(i, contagion_state)]
    if DISPLAY:
        display(md("From which %i individuals are infected"%(len(individuals_infected_gotostore))))
    
    # Stores that will be visited by a contagious person
    infected_stores = [map_houses_stores[map_individuals_houses[i]] for i in individuals_infected_gotostore]
    if DISPLAY:
        display(md("%i grocerie stores are infected"%(len(infected_stores))))
    
    # People who live in a house that goes to a contagious store
    individuals_attachedto_infected_store = flatten(flatten(
        [[map_houses_adults[h] for h in map_stores_houses[s]] for s in infected_stores]))
    
    # People who did go to that contagious store
    individuals_goto_infected_store = list(set(individuals_attachedto_infected_store)
                                           .intersection(set(individuals_gotostore)))
    if DISPLAY:
        display(md("%i individuals went to an infected store"%(len(individuals_goto_infected_store))))
    
    # People who got infected from going to their store
    infected_backfromstore = [i for i in individuals_goto_infected_store if getR() < PROB_INFECTION_AT_STORE]
    
    # INFECTION STATE UPDATE
    updateInfectionPeriod(infected_backfromstore, infection_state, contagion_state)
    if DISPLAY:
        display(md("Ending at the morning with %i infected individuals"%(len(getInfectedPeople(infection_state)))))

Let’s innoculate 0.5% of the population the COVID-19 and start

inn_ind_cov = dict(zip(range(N), [int(getR() <= 0.005) for i in range(N)]))

# Infection dictionnary initialization
all_ind_inf = dict(zip(range(N), [-1]*N))
all_ind_con = dict(zip(range(N), [-1]*N))
ind_infected_init = [k for k,v in inn_ind_cov.items() if v==1]

for ind in ind_infected_init:
    # Incubation period between 2 and 14 days
    incubation, contagiosity = getInfectionParameters()
    all_ind_inf[ind] = incubation
    all_ind_con[ind] = contagiosity

living_infected_individuals_at_20pm = ind_infected_init

display(md("We start our cycle with %i infected individuals"%(len(getInfectedPeople(all_ind_inf)))))

We start our cycle with 31 infected individuals

Let’s start the infection cycle

stats = []
for _ in range(N_days):
    # INFECTION AT HOME
    propagateToHouses(all_ind_hou, all_hou_ind, all_ind_inf, all_ind_con)
    propagateToWorkplaces(all_ind_wor, all_wor_ind, all_ind_inf, all_ind_con)
    propagateToGroStores(all_ind_hou, all_hou_sto, all_sto_hou, all_hou_adu, all_ind_inf, all_ind_con)
    incrementInfectionDay(all_ind_inf, all_ind_age, all_ind_con)
    stats.append((len(getHealthyPeople(all_ind_inf)), 
                  len(getInfectedPeople(all_ind_inf)), 
                  len(getDeadPeople(all_ind_inf)),
                  len(getImmunePeople(all_ind_inf))))

Some plots

fig, ax = plt.subplots(figsize=(15, 10))

healthySerie = [stats[i][0] for i in range(N_days)]

infectedSerie = [stats[i][1] for i in range(N_days)]

deadSerie = [stats[i][2] for i in range(N_days)]
deadSerieStack = [stats[i][0] + stats[i][1] for i in range(N_days)]

immuneSerie = [stats[i][3] for i in range(N_days)]
immuneSerieStack = [stats[i][0] + stats[i][1] + stats[i][2] for i in range(N_days)]

ind = np.arange(N_days)
width = 0.6

p1 = plt.bar(ind, healthySerie, width, color="#3F88C5")
p2 = plt.bar(ind, infectedSerie, width, bottom=healthySerie, color="#A63D40")
p3 = plt.bar(ind, deadSerie, width, bottom=deadSerieStack, color="#151515")
p4 = plt.bar(ind, immuneSerie, width, bottom=immuneSerieStack, color="#90A959")

plt.ylabel('Population')
plt.title('Pandemic evolution')
plt.xticks(np.arange(0, N_days, int(N_days/10)), tuple([('Day ' + str(10*i)) for i in range(int(N_days/10))]))
plt.yticks(np.arange(0, N, N/25))
plt.legend((p1[0], p2[0], p3[0], p4[0]), ('Healthy', 'Infected', 'Dead', 'Immune'))

plt.show()

fig, ax = plt.subplots(figsize=(15, 10))

healthySerie = [stats[i][0] for i in range(N_days)]
newCasesSerie = list([j-i for (i,j) in zip(healthySerie[1:], healthySerie[:-1] )])

ind = np.arange(N_days-1)
width = 0.6

p1 = plt.bar(ind, newCasesSerie, width, color="#44A1A0")

plt.ylabel('Population')
plt.title('New infected cases evolution')
plt.xticks(np.arange(0, N_days-1, int(N_days/10)), tuple([('Day ' + str(10*i)) for i in range(int(N_days/10))]))
plt.yticks(np.arange(0, int(max(newCasesSerie)*1.1), 5))
plt.legend((p1[0],), ('New cases',))

plt.show()

Sources

• Répartition démographique de l’âge : https://www.populationpyramid.net/world/2019/
• Taux de mortalité du Coronavirus : https://www.worldometers.info/coronavirus/coronavirus-age-sex-demographics/
• Répartition des tailles d’entreprises au Maroc : https://fnh.ma/article/actualite-economique/les-tpme-representent-93-des-entreprises-marocaines-en-2019